
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Квадратурная формула Симпсона (парабол)
|
|
|
|
Упражнения.
5.5 Вычислить по квадратурной формуле трапеций при n = 3 интеграл и сравнить с точным значением интеграла:
а) 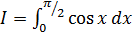 , I = 1; б)
, I = 1; б) 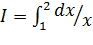 , I = ln 2;
, I = ln 2;
в) 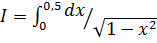 , I =
, I = 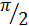 ; г)
; г)  , I = 0,75.
, I = 0,75.
5.6 Вычислить по квадратурной формуле трапеций при n = 5 интеграл и оценить погрешность интегрирования:
а) 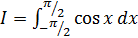 ; б)
; б)  ;
;
в) 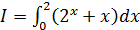 ; г)
; г) 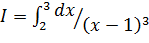 .
.
5.7 Определить число узлов n, которое нужно использовать для вычисления интеграла с помощью формулы трапеций с точностью до 0,01:
а) 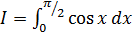 ; б)
; б) 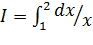 ; в)
; в) 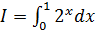 ; г)
; г) 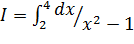 .
.
5.8 Вычислить по квадратурной формуле трапеций интеграл с точностью до 0,01:
а) 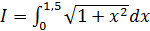 ; б)
; б) 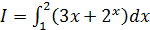 ;
;
в)  ; г)
; г) 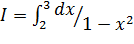 .
.
При выводе квадратурной формулы трапеций (16) было использовано кусочно-линейное интерполирование подынтегральной функции 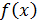 на отрезке
на отрезке 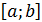 функцией (13).
функцией (13).
Вывод квадратурной формулы Симпсона (парабол) развивает описанный подход. Теперь для аппроксимации[26] функции 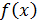 на отрезке
на отрезке 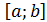 используем не кусочно-линейное, а кусочно-квадратичное интерполирование.
используем не кусочно-линейное, а кусочно-квадратичное интерполирование.
Для этого будем считать n четным и сгруппируем отрезки 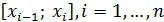 парами: первая пара
парами: первая пара 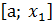 и
и 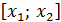 , вторая пара
, вторая пара 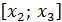 и
и 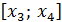 и т.д. Для каждого двойного отрезка
и т.д. Для каждого двойного отрезка 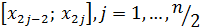 построим интерполяционный многочлен второй степени в форме Лагранжа, принимающий в узлах
построим интерполяционный многочлен второй степени в форме Лагранжа, принимающий в узлах 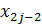 ,
, 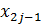 и
и 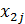 значения функции
значения функции 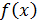 . В результате получим аппроксимирующую функцию
. В результате получим аппроксимирующую функцию 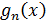 на отрезке
на отрезке 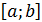 в виде кусочно-квадратичной функции:
в виде кусочно-квадратичной функции:
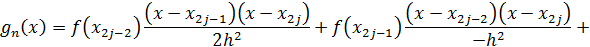
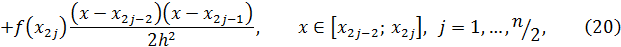
где  .
.
Проинтегрировав функцию 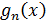 по отрезку
по отрезку 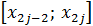 , получим
, получим
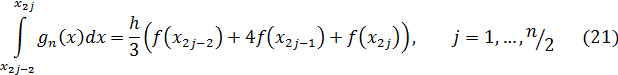
Интеграл от функции 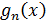 по всему отрезку
по всему отрезку 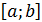 равен сумме интегралов (21)
равен сумме интегралов (21)
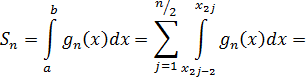
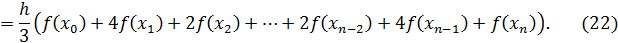
Замечание. В равенстве (22) число n должно быть четным.
Величина 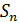 (22) дает приближенное значение интеграла I:
(22) дает приближенное значение интеграла I:
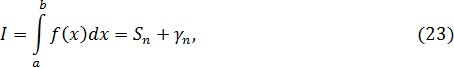
где 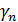 – остаточный член квадратурной формулы. Узлами формулы (23), как и квадратурной формулы трапеции (16), являются точки
– остаточный член квадратурной формулы. Узлами формулы (23), как и квадратурной формулы трапеции (16), являются точки 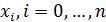 . Весовые коэффициенты в узлах с четными и нечетными номерами имеют разные значения (у узлов с четными номерами веса равны
. Весовые коэффициенты в узлах с четными и нечетными номерами имеют разные значения (у узлов с четными номерами веса равны 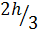 кроме узлов
кроме узлов 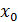 и
и 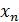 у которых веса равны
у которых веса равны 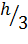 , а у узлов с нечетными номерами веса равны
, а у узлов с нечетными номерами веса равны 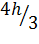 . Формула (23) называется квадратурной формулой Симпсона (парабол).
. Формула (23) называется квадратурной формулой Симпсона (парабол).
Представление (22) для 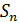 , как и представление (15) для
, как и представление (15) для 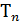 , также можно рассматривать как интегральную сумму функции
, также можно рассматривать как интегральную сумму функции 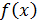 на отрезке
на отрезке 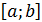 . Поэтому, если функция
. Поэтому, если функция 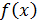 интегрируема на
интегрируема на 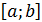 , то в силу определения определенного интеграла
, то в силу определения определенного интеграла
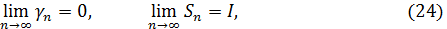
т.е. условия сходимости квадратурной формулы Симпсона (парабол) (24) в этом случае выполняются.
Рассмотрим основной вопрос, связанный с организацией реального вычислительного процесса: каким нужно взять n, чтобы добиться при вычислении определенного интеграла (6) требуемой точности ε. Для этого необходимо провести оценку остаточного члена (погрешности) 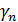 . В связи с этим подынтегральная функция
. В связи с этим подынтегральная функция 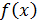 должна быть не только интегрируема, но и четырежды непрерывно дифференцируема на отрезке
должна быть не только интегрируема, но и четырежды непрерывно дифференцируема на отрезке 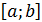 . Если выполняются все описанные выше условия, то для остаточного члена
. Если выполняются все описанные выше условия, то для остаточного члена 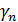 имеет место следующая оценка
имеет место следующая оценка

где Мʹ – положительное число ограничивающее четвертую производную подынтегральной функции 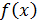 на отрезке
на отрезке 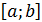 , т.е.
, т.е. 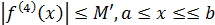 .
.
При заданной точности ε условие (25) позволяет определить число узлов n, которое нужно использовать при вычислении определенного интеграла (6). Для этого достаточно использовать соотношение

Пример 1. Вычислить по квадратурной формуле Симпсона (парабол) при n = 2 интеграл

Сравнить с точным значением интеграла.
Решение.
Так как n = 2, то шаг
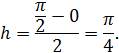
Найдем значения 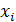 ,
, 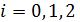 используя соотношение
используя соотношение 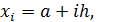
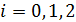 и учитывая, что
и учитывая, что 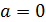 и
и 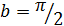 :
:
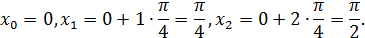
Теперь вычислим значения подынтегральной функции 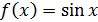 в точках
в точках 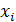 ,
, 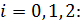
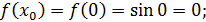
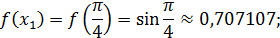
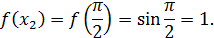
Значит по формуле (22) имеем
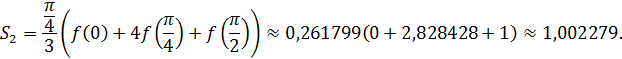
Следовательно, 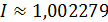 .
.
Сравним полученное приближенное значение с точным значением интеграла

 .
.
Ответ: 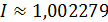 ,
, 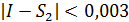 .
.
Пример 2. Определить число узлов n, которое нужно использовать для вычисления интеграла с помощью формулы Симпсона (парабол)
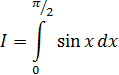
с точностью до 0,001.
Решение.
Для определения n, воспользуемся формулой (26)
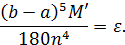
По условию задачи 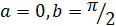 и ε = 0,001. Учитывая, что подынтегральная функция
и ε = 0,001. Учитывая, что подынтегральная функция 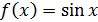 и ее первая, вторая, третья и четвертая производные соответственно равны
и ее первая, вторая, третья и четвертая производные соответственно равны  ,
, 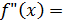
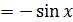 ,
, 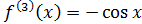 и
и 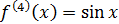 то на отрезке интегрирования
то на отрезке интегрирования 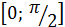 справедливо
справедливо 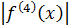 =
= 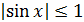 . Значит
. Значит 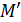 = 1. В результате получим соотношение
= 1. В результате получим соотношение
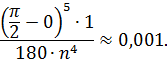
Решая которое определим n:
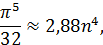
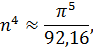
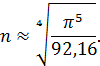
Так как
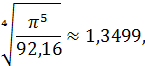
а 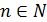 , то возьмем n = 2.
, то возьмем n = 2.
Следовательно, чтобы достичь точности ε = 0,001, необходимо взять 3 узла.
Ответ: n = 2.
Пример 3. Вычислить по квадратурной формуле трапеции Симпсона (парабол)

с точностью до 0,01.
Решение.
Определим сначала число узлов n, которое необходимо использовать для вычисления интеграла. По условию задачи  , ε = 0,01 и
, ε = 0,01 и  . Так как
. Так как
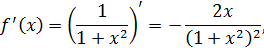
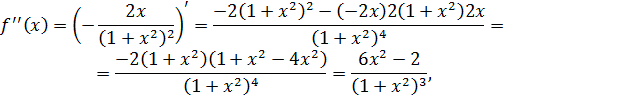
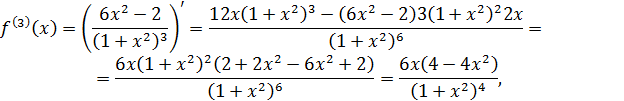
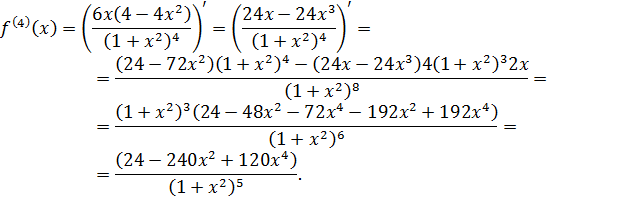
и для  выполняется
выполняется
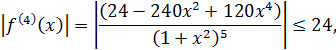
то 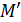 = 24. Подставляя значения a, b, ε и М в формулу (26) получим соотношение:
= 24. Подставляя значения a, b, ε и М в формулу (26) получим соотношение:
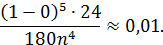
Из которого найдем n.
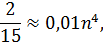
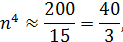
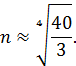
Так как
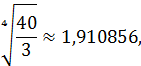
а 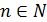 , то возьмем n = 2.
, то возьмем n = 2.
Так как n = 2, то шаг

Найдем значения 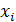 ,
, 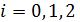 используя соотношение
используя соотношение 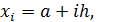
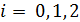 и учитывая, что
и учитывая, что 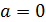 , а b
, а b 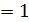 :
:
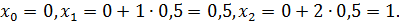
Теперь вычислим значения подынтегральной функции 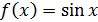 в точках
в точках 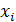 ,
, 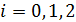 :
:
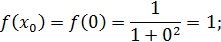
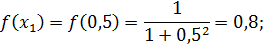
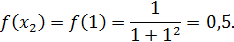
Значит по формуле (22) имеем
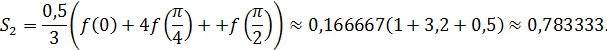
Следовательно, 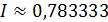 .
.
Ответ: 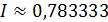 с точностью до 0,01.
с точностью до 0,01.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1286; Нарушение авторских прав?; Мы поможем в написании вашей работы!