
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Апостериорные оценки погрешности при численном интегрировании
|
|
|
|
Упражнения.
5.9 Вычислить по квадратурной формуле Симпсона при n = 4 интеграл и сравнить с точным значением интеграла:
а) 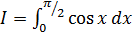 , I = 1; б)
, I = 1; б) 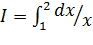 , I = ln 2;
, I = ln 2;
в) 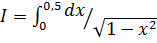 , I =
, I = 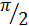 ; г)
; г)  , I = 0,75.
, I = 0,75.
5.10 Вычислить по квадратурной формуле Симпсона при n = 4 интеграл и оценить погрешность интегрирования:
а) 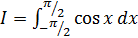 ; б)
; б) 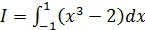 ;
;
в) 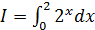 ; г)
; г) 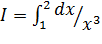 .
.
5.11 Определить число узлов n, которое нужно использовать для вычисления интеграла с помощью формулы Симпсона с точностью до 0,01:
а)  ; б)
; б) 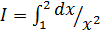 ; в)
; в) 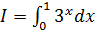 ; г)
; г) 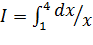 .
.
5.12 Вычислить по квадратурной формуле Симпсона интеграл с точностью до 0,01:
а)  ; б)
; б) 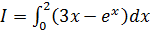 ;
;
в) 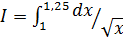 ; г)
; г) 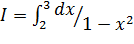 .
.
В латинском языке существуют два термина – антонима: априори (a priori) и апостериори (a posteriori). Первый означает изначально, независимо от опыта, второй – на основании опыта. Оба они часто используются в вычислительной математике, подразделяя информацию на ту, которая известна до начала вычислений, и ту, которая получается в процессе вычислений.
Оценки погрешности квадратурных формул прямоугольников (8), трапеций (16), Симпсона (23) называют априорными. Они справедливы изначально и предсказывают точность вычисления интеграла (6) независимо от того, будем мы фактически проводить вычисления или нет. Эти результаты позволяют понять структуру остаточных членов, определить скорость их убывания при возрастании n.
Но в процессе вычисления погрешностей 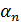 ,
, 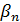 и
и 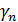 приходится определять константы М и M ʹ, ограничивающие вторую и четвертую производные подынтегральной функции
приходится определять константы М и M ʹ, ограничивающие вторую и четвертую производные подынтегральной функции 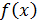 по абсолютной величине на отрезке интегрирования
по абсолютной величине на отрезке интегрирования 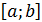 . Чтобы это сделать приходится проводить дополнительные исследования функции
. Чтобы это сделать приходится проводить дополнительные исследования функции 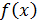 , в частности, находить производные соответствующих порядков, что требует определенных усилий и времени. При этом если
, в частности, находить производные соответствующих порядков, что требует определенных усилий и времени. При этом если 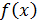 задается графиком, таблицей и т.п., то возникают большие даже непреодолимые трудности.
задается графиком, таблицей и т.п., то возникают большие даже непреодолимые трудности.
В связи с этим рассмотрим методы оценки погрешности численного интегрирования, которые не требуют предварительного анализа производных подынтегральной функции. Они основаны на сопоставлении результатов вычислений с разным числом узлов n и называются апостериорными.
Для рассмотренных квадратурных формул имеют место следующие апостериорные оценки погрешностей:
- формула прямоугольников 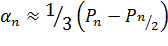 ; (27)
; (27)
- формула трапеций 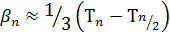 ; (28)
; (28)
- формула Симпсона 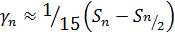 . (29)
. (29)
Замечание. В формулах (27) – (28) необходимо чтобы число n было четным.
Пример 1. Вычислить по квадратурной формуле Симпсона (парабол) при n = 4 интеграл

Используя результаты примера 1 из п. 5.4., найти приближенную апостериорную погрешность.
Решение.
Так как n = 4, то шаг

Найдем значения 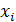 ,
, 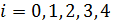 используя соотношение
используя соотношение  и учитывая, что
и учитывая, что 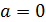 и
и 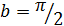 :
:
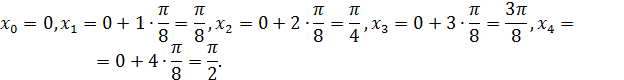
Теперь вычислим значения подынтегральной функции 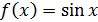 в точках
в точках 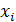 ,
, 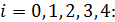
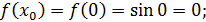

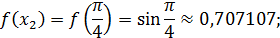
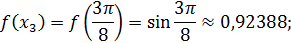
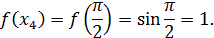
Значит по формуле (22) имеем
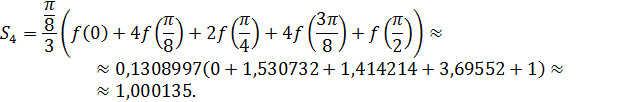
Следовательно,  .
.
Найдем погрешность
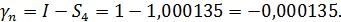
Теперь определим апостериорную оценку погрешности по результатам двух расчетов 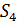 и
и 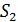 по формуле (29):
по формуле (29):
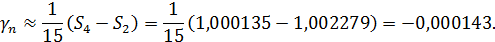
Как видим она согласуется с фактической погрешностью, сосчитанной по известному значению интеграла.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1178; Нарушение авторских прав?; Мы поможем в написании вашей работы!