
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Квадратурная формула трапеций
|
|
|
|
Упражнения.
5.1 Вычислить по квадратурной формуле прямоугольников при n = 3 интеграл и сравнить с точным значением интеграла:
а) 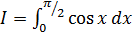 , I = 1; б)
, I = 1; б) 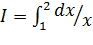 , I = ln 2;
, I = ln 2;
в) 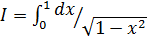 , I =
, I = 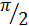 ; г)
; г)  , I = 0,75.
, I = 0,75.
5.2 Вычислить по квадратурной формуле прямоугольников при n = 5 интеграл и оценить погрешность интегрирования:
а) 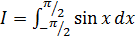 ; б)
; б) 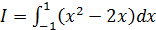 ;
;
в) 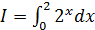 ; г)
; г) 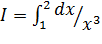 .
.
5.3 Определить число узлов n, которое нужно использовать для вычисления интеграла с помощью формулы прямоугольников с точностью до 0,01:
а) 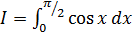 ; б)
; б) 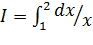 ; в)
; в) 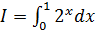 ; г)
; г)  .
.
5.4 Вычислить по квадратурной формуле прямоугольников интеграл с точностью до 0,01:
а) 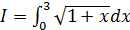 ; б)
; б) 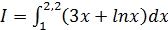 ;
;
в)  ; г)
; г) 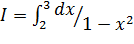 .
.
Рассмотрим определенный интеграл I (6) и изобразим график подынтегральной функции 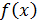 (рис. 17). Разобьем отрезок интегрирования
(рис. 17). Разобьем отрезок интегрирования 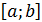 на n равных отрезков точками
на n равных отрезков точками 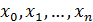 , где
, где 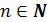 (рис. 17).
(рис. 17).
| Рисунок 17 |
| f (х 1) |
| f (х 2) |
| f (хi) |
| f (хn -1) |
| f (хn) |
| f (х 0) |
| f (хi -1) |
| f (хn- 2) |
| x 0 |
| x 1 |
| x 2 |
| xi-1 |
| xi |
| xn-1 |
| xn |
| xn-2 |
| а |
| b |
| х |
| у |
| О |
Длина каждого отрезка разбиения  . При этом очевидно, что для точек разбиения
. При этом очевидно, что для точек разбиения 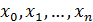 будет справедливо соотношение:
будет справедливо соотношение:
 ,
,
причем x 0 = a и xn = b.
Соединим отрезками точки графика функции 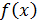 с координатами
с координатами 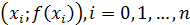 . В результате получим ломанную, которая является графиком кусочно-линейной функции
. В результате получим ломанную, которая является графиком кусочно-линейной функции 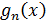 (рис. 17). На каждом из отрезков разбиения
(рис. 17). На каждом из отрезков разбиения 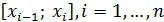 функция
функция 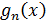 задается формулой
задается формулой
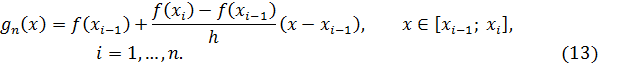
В точках 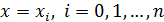 она принимает те же значения, что и функция
она принимает те же значения, что и функция 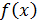 :
:
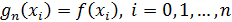 ,
,
т.е. функция 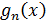 осуществляет кусочно-линейную интерполяцию функции
осуществляет кусочно-линейную интерполяцию функции 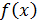 на отрезке
на отрезке 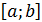 (рис 17).
(рис 17).
Вычислим интеграл:
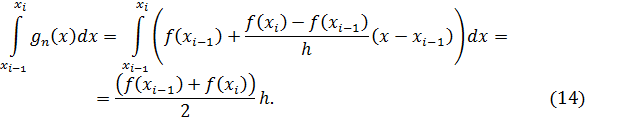
Этот результат имеет простой геометрический смысл: фигура, ограниченная снизу отрезком 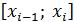 оси Ох, сверху отрезком функции (13), с боков вертикальными прямыми
оси Ох, сверху отрезком функции (13), с боков вертикальными прямыми 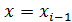 и
и 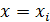 , представляет собой трапецию с основаниями длины
, представляет собой трапецию с основаниями длины 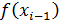 и
и 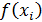 и высотой h, площадь которой определяется формулой (14) (рис. 17).
и высотой h, площадь которой определяется формулой (14) (рис. 17).
Интеграл от функции 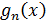 по всему отрезку
по всему отрезку 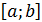 является суммой интегралов (14):
является суммой интегралов (14):
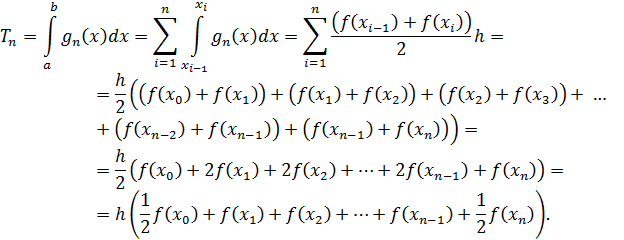
Квадратурная формула
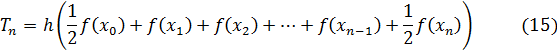
дает приближенное значение интеграла I:
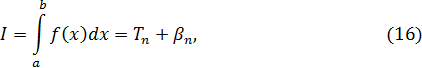
где 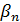 – остаточный член (специальное обозначение). В квадратурной формуле (16), которая называется квадратурной формулой трапеций, узлами являются точки
– остаточный член (специальное обозначение). В квадратурной формуле (16), которая называется квадратурной формулой трапеций, узлами являются точки 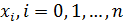 , весовые множители все, кроме двух при
, весовые множители все, кроме двух при 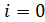 и
и 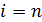 , одинаковы и равны
, одинаковы и равны  , а весовые коэффициенты при
, а весовые коэффициенты при 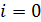 и
и 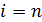 равны
равны 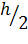 . С точностью до
. С точностью до 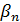 формула (16) выражает площадь криволинейной трапеции, соответствующую интегралу I, через сумму площадей трапеций (14) (рис. 17).
формула (16) выражает площадь криволинейной трапеции, соответствующую интегралу I, через сумму площадей трапеций (14) (рис. 17).
Формула (7) или (7ʹ) для величины  строилась как интегральная сумма. При выводе формулы (15) для
строилась как интегральная сумма. При выводе формулы (15) для 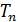 понятие интегральной суммы не использовалось, но ее так же можно рассматривать как интегральную сумму. Следовательно, если функция
понятие интегральной суммы не использовалось, но ее так же можно рассматривать как интегральную сумму. Следовательно, если функция 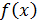 интегрируема на
интегрируема на 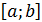 , то в силу определения определенного интеграла
, то в силу определения определенного интеграла
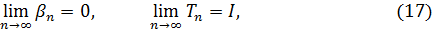
т.е. условия сходимости квадратурной формулы трапеций (16) в этом случае выполняются.
Предельные соотношения (17) доказывают принципиальную возможность вычисления определенного интеграла от произвольной интегрируемой функции методом трапеции с любой точностью ε за счет выбора числа n точек разбиения отрезка 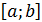 и соответствующего шага h.
и соответствующего шага h.
Рассмотрим основной вопрос, связанный с организацией реального вычислительного процесса: каким нужно взять n, чтобы добиться при вычислении определенного интеграла (6) требуемой точности ε. Для этого необходимо провести оценку остаточного члена (погрешности) 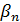 . В связи с этим подынтегральная функция
. В связи с этим подынтегральная функция 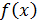 должна быть не только интегрируема, но и дважды непрерывно дифференцируема на отрезке
должна быть не только интегрируема, но и дважды непрерывно дифференцируема на отрезке 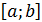 . Если выполняются все описанные выше условия, то для остаточного члена
. Если выполняются все описанные выше условия, то для остаточного члена 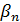 имеет место следующая оценка
имеет место следующая оценка

где М – положительное число удовлетворяющее условию (11).
При заданной точности ε условие (18) позволяет определить число узлов n, которое нужно использовать при вычислении определенного интеграла (6). Для этого достаточно использовать соотношение

Пример 1. Вычислить по квадратурной формуле трапеций при n = 3 интеграл

Сравнить с точным значением интеграла.
Решение.
Так как n = 3, то шаг
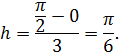
Найдем значения 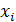 ,
, 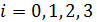 используя соотношение
используя соотношение 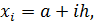
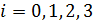 и учитывая, что
и учитывая, что 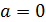 и
и 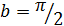 :
:
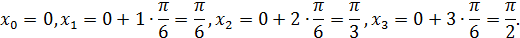
Теперь вычислим значения подынтегральной функции 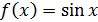 в точках
в точках 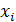 ,
, 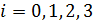 :
:
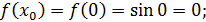
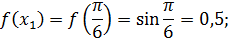
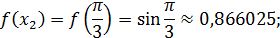
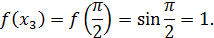
Значит по формуле (15) имеем
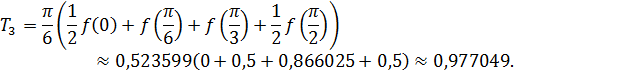
Следовательно, 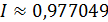 .
.
Сравним полученное приближенное значение с точным значением интеграла

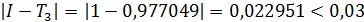 .
.
Ответ: 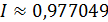 ,
, 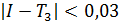 .
.
Пример 2. Определить число узлов n, которое нужно использовать для вычисления интеграла с помощью формулу трапеций
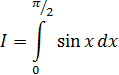
с точностью до 0,01.
Решение.
Для определения n, воспользуемся соотношение (19)
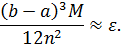
По условию задачи 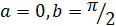 и ε = 0,01. Учитывая, что подынтегральная функция
и ε = 0,01. Учитывая, что подынтегральная функция 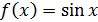 и ее первая и вторая производные соответственно равны
и ее первая и вторая производные соответственно равны  и
и 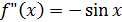 , то на отрезке интегрирования
, то на отрезке интегрирования 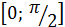 справедливо
справедливо 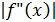 =
= 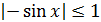 . Значит М = 1. В результате получим соотношение
. Значит М = 1. В результате получим соотношение
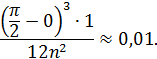
Из которого определим n:
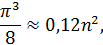
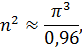
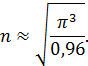
Так как
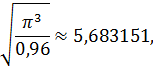
а 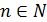 , то возьмем n = 6.
, то возьмем n = 6.
Следовательно, чтобы достичь точности ε = 0,01, необходимо взять 7 узлов.
Ответ: n = 6.
Пример 3. Вычислить по квадратурной формуле трапеций интеграл

с точностью до 0,01.
Решение.
Определим сначала число узлов n, которое необходимо использовать для вычисления интеграла. По условию задачи  , ε = 0,01 и
, ε = 0,01 и  . Так как
. Так как
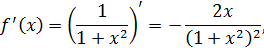
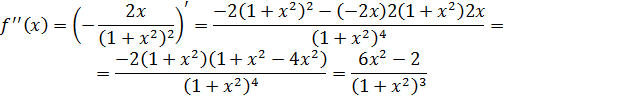
и для  выполняется
выполняется
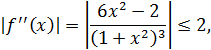
то М = 2. Подставляя значения a, b, ε и М в формулу (12) получим соотношение:
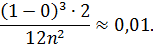
Из которого найдем n.
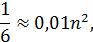
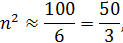
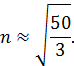
Так как
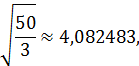
а 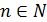 , то возьмем n = 5.
, то возьмем n = 5.
Так как n = 5, то шаг
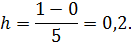
Найдем значения 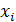 ,
, 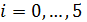 используя соотношение
используя соотношение 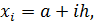
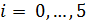 и учитывая, что
и учитывая, что 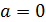 , а b
, а b 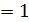 :
:
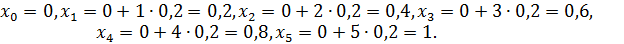
Теперь вычислим значения подынтегральной функции 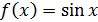 в точках
в точках 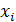 ,
, 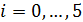 :
:
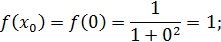
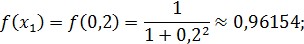
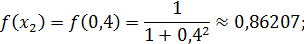
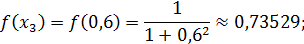
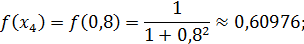
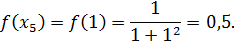
Значит по формуле (15) имеем
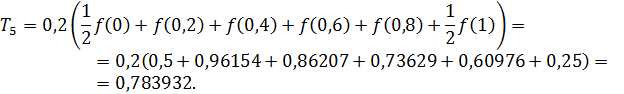
Следовательно, 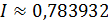 .
.
Ответ: 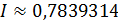 с точностью до 0,01.
с точностью до 0,01.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2070; Нарушение авторских прав?; Мы поможем в написании вашей работы!