
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод математической индукции
|
|
|
|
Определение целого неотрицательного числа.
Тема 2. Аксиоматический метод в математике. Аксиомы Пеано.
Контрольные вопросы по теории
1. В чем суть аксиоматического способа построения математической теории?
2. Каковы особенности основных понятий и аксиом?
3. Какие требования предъявляются к системе аксиом?
4. Какое предложение называют теоремой?
5. Назовите основные понятия и отношения аксиоматической теории целых неотрицательных чисел.
6. Сформулируйте аксиомы, которым удовлетворяет отношение «непосредственно следовать за» для целых неотрицательных чисел.
7. Дайте определение отрезка натурального ряда чисел и запишите множества N2, N8.
8. Что значит «пересчитать» элементы конечного множества?
9. Раскройте понятие целого неотрицательного числа с теоретико-множественной точки зрения.
10. Сформулируйте принцип полной математической индукции.
11. Опишите в общем виде процесс доказательства методом математической индукции. Из скольких этапов он состоит?
Практические задания
1. Элементами множества являются группы черточек
{І, ІІ, ІІІ, ІІІІ, …}. Как можно определить здесь отношение «следует за»? Удовлетворяет ли оно аксиомам Пеано?
2. Задайте отношение «следует за» на множестве {3, 4, 5, 6, …}? Удовлетворяет ли оно аксиомам Пеано? Какой элемент является здесь начальным?
3. Можно ли на множестве {…, – n,…, –3, –2, –1, 0, 1, …, n, …} задать отношение «следует за», удовлетворяющее аксиомам Пеано?
4. Удовлетворяют ли множества аксиомам Пеано? Какие условия здесь нарушены?

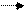
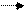

 а) b б) b d … в) с
а) b б) b d … в) с

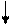
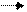

 а а а b
а а а b
 |

 с с е … d
с с е … d
5. Постройте систему, удовлетворяющую аксиоме 1 и не удовлетворяющую аксиомам 2 и 3.
6. Постройте систему, удовлетворяющую аксиоме 2 и не удовлетворяющую аксиоме 1.
7. Постройте систему, удовлетворяющую аксиомам 1 и 2 и не удовлетворяющую аксиоме 3.
8. Запишите все элементы множеств N8, N1. Как называются эти множества?
9. Можно ли назвать отрезками натурального ряда множества:
а) {0; 1; 2; 3}; б) {1; 3; 5; 7}; в) {1; 2; 3}; г) {3; 4; 5}?
10. Существует ли отрезок натурального ряда длины 0?
11. На столе лежат букварь и учебник по математике. Запишите множество А книг, которые лежат на столе. Назовите еще три множества, которые равномощны множеству А. Какое натуральное число является общим свойством класса множеств, равномощных множеству А?
12. Придумайте множества С и D, для которых выполняются условия: а) n (C) = n (D) и C ≠ D; б) n (C) = n (D) и C = D.
13. Приведите примеры множеств, равномощных:
а) множеству А – глаз у человека;
б) множеству В – спутников Земли;
в) множеству С – землян, побывавших на Марсе;
г) назовите общее свойство класса множеств, представителем которого является множество А, В, С.
14. Прочитайте записи: n (A) = 5; n (B) = 1; n (C) = 0. Приведите примеры множеств А, В и С, удовлетворяющих этим условиям. В какой роли здесь выступают целые неотрицательные числа 5, 1, 0?
15. Найдите n (А), если А: а) множество граней куба;
б) множество ребер куба; в) множество вершин куба. Приведите примеры множеств, равномощных множеству А.
16. Найдите численность множеств:
а) А = { x ÷ x 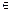 N 0, х < 10}; в) С = { x ç x
N 0, х < 10}; в) С = { x ç x 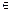 N 0, 0 < x < 1};
N 0, 0 < x < 1};
б) В = { x ç x 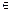 N 0, x < 1}; г) D = { x ç x
N 0, x < 1}; г) D = { x ç x 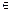 N 0, x ≤ 0}?
N 0, x ≤ 0}?
17. Почему на уроке, где изучается число «три», можно использовать картину с изображением трёх яблок, трёх тетрадей, а можно воспользоваться и другими примерами трёхэлементных множеств?
18. Приведите примеры множеств, являющихся представителями класса непустых конечных множеств, общим свойством которых является натуральное число 4.
19. Сформулируйте условия, которые необходимо соблюдать, ведя счет элементов конечного множества.
20. Из учебников по математике для начальных классов приведите примеры двух заданий, в которых число выступает как:
а) порядковое; б) количественное.
21. Подберите формулу n -го члена последовательности:
а) 2; 4; 6; 8; …;
б) 1; 3; 5; 7; 9;…;
в) 5; 10; 15; 20; 25; …;
г) 1; 4; 9; 16; 25; …;
д) 1; 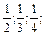 …;
…;
е) 1; – 2; 3; – 4; 5; – 6; …;
ж) 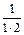 ;
; 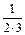 ;
; 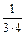 ;
; 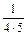 ; …;
; …;
з) 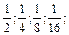 …
…
22. Напишите первый, k -й и (k +1) член последовательности, заданный формулой ее n- го члена:
а) n 3 ; б) 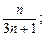 в)
в) 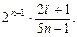
23. Разложите на множители выражение:
а) k2 + 2 k;
б) 3 k (k +1) + (k +1)2;
в) 4 k 2 + 4 k +1;
г) k 2 – 6 k + 9;
д) k 2 – 3 k + 2;
е) 2 k 2 + 7 k + 6;
ж) 7 k 2 – 3 k –10;
з) 2 k 2 + 3 k + 1.
24. Докажите, что сумма n первых членов натурального ряда равна 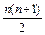 .
.
25. Докажите, что сумма квадратов n первых натуральных чисел равна  .
.
26. Докажите, что для любого натурального числа n справедливо равенство:
а)13 + 23 + 33 + … + n 3 = 
б) 1 + 3 + 6 + 10 + … + 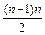 +
+  =
= 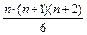 ;
;
в) 1 ∙ 2 + 2 ∙ 5 + 3 ∙ 8 +… + n ∙ (3 n – 1) = n 2 ∙ (n +1);
г) 1 ∙ 4 + 2 ∙ 7 + 3 ∙10 + … + n (3 n + 1) = n (n + 1)2;
д) 1 ∙ 2 + 2 ∙ 3 + … + n ∙ (n +1) ∙ = 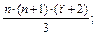
е) 1 ∙ 2 ∙ 3 + 2 ∙ 3 ∙ 4 + … + n (n +1)(n +2)= 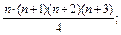
ж) 
з) 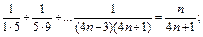
и) 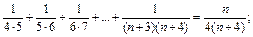
к) 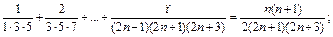
л) (1 – 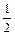 )(1 –
)(1 – 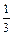 ) ∙ … ∙ (1 –
) ∙ … ∙ (1 – 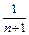 ) =
) = 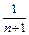 ;
; 
м) (1 – 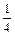 )(1 –
)(1 – 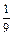 ) … (1 –
) … (1 – 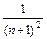 ) =
) = 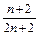 ;
;
27. Чему равна сумма первых n нечетных натуральных чисел?
28. Докажите неравенство:
а) 2 п ≥ n + 1, n 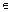 N;
N;
б) 2 n +4 > (n + 4)2, n 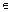 N;
N;
в) 4 п > 7 n – 5, n 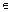 N;
N;
г) 2 n > 5 n + 1, где n 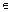 N, n ≥ 5;
N, n ≥ 5;
29. Докажите, что при любом натуральном n > 1 число 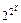 + 1 оканчивается цифрой 7.
+ 1 оканчивается цифрой 7.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 3725; Нарушение авторских прав?; Мы поможем в написании вашей работы!