Тема 4. Сложение на множестве целых неотрицательных чисел

Контрольные вопросы по теории

1. Сформулируйте определение сложения целых неотрицательных чисел и докажите, что каждое целое неотрицательное число получается из предыдущего прибавлением единицы.

2. Докажите, что при любом а Î N₀: а) 0 + а = а, б) 1 + а = а + 1.

3. Дайте теоретико-множественное истолкование суммы двух целых неотрицательных чисел. Объясните, почему сумму чисел связывают с объединением непересекающихся множеств, а не множеств вообще.

4. Сформулируйте свойства операции сложения. Докажите ассоциативный и коммутативный законы с двух точек зрения (аксиоматической и теоретико-множественной). Какие преобразования выражений возможны на основании этих законов?

Практические задания

1. Используя определение сложения, найдите значение выражений: а) 3 + 2; б) 3 + 3; в) 4 + 3.

2. Какие условия надо наложить на множества А и В, чтобы были истинными высказывания:

а) n (A) + n (B) > n (A B);

б) n (A) + n (B) = n (A B);

в) n (A) + n (B) = n (A).

3. Каков теоретико-множественный смысл суммы: а) 3 + 5;
б) 0 + 4; в) 0 + 0.

4. Каждой паре из множества A ={(3; 0); (4; 7); (1; 1); (5; 6)} поставлено в соответствие натуральное число по следующему правилу: паре (а; b) соответствует сумма чисел а и b. Запишите множество B, на которое отобразилось множество A. Постройте граф отображения.

5. Какие высказывания истинны? Объясните почему.

а) (" а Î N₀) ($ b Î N₀) a + b = a;

б) (" а Î N₀) ($ b Î N) a + b = a;

в) ($ а, b Î N₀) a + b = a;

г)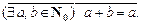

6. Дайте теоретико-множественное истолкование суммы k слагаемых, используя полученный вывод, объясните теоретико-множественный смысл суммы: а) 3 + 4 +2; б) 1 +2 +3 + 4.

7. Найдите в учебнике математики для 1 класса упражнения, в которых раскрывается конкретный смысл действия сложения. Объясните их, используя теоретико-множественный подход.

8. Чем вызвана необходимость изучения переместительного свойства сложения перед изучением сложения чисел второго «пятка» и какова методика ознакомления с этим свойством?

9. Изучаются ли ассоциативный закон сложения в курсе математики начальной школы?

10. Выясните, как формулируются в различных учебниках математики для начальной школы коммутативное и ассоциативное свойства сложения.

11. Какие преобразования выражений можно выполнять, используя свойство ассоциативности сложения?

12. Выполните преобразование выражения, применив ассоциативное свойство сложения:

а) (12 +3)+17; б) 24 + (6 +19); в) 27 + 13 +18.

13. Применяя ассоциативный и коммутативный законы сложения, преобразуйте выражения и найдите их значения:

а) 63521 + 37542 + 36479;

б) 48597 + 62473 + 37527;

в) 34856 + (15144 +69837);

г) (63436 + 23876) + 76544;

д) 8687 + 4735 + 5265 + 1313;

е) 1264 + 1236 + 2500+ 7393.

14. Вычислите удобным способом:

а) 41989 + (98999 + 58 011);

б) (97381 + 69737) + 32681;

в) 4875 + 3967 + 5125 + 6033;

г) 84973 + 1142 + 13027 + 4858.

15. Решите 5 примеров из учебников математики для начальной школы, в которых переместительное и сочетательное свойства сложения используются одновременно.

16. Как изменится сумма при увеличении (уменьшении) одного из слагаемых? Найдите в учебниках математики начальной школы упражнения, которые раскрывают эту зависимость.

17. Заполни таблицу:

	1-е слагаемое	2-е слагаемое	Сумма
1.	+ 13	+29	?
2.	–17	–9	?
3.	+36	–14	?
4.	–56	+19	?
5.	+12	?	–19
6.	–25	?	–34

18. Известно, что a + b =17. Чему равно:

а) a + (b + 3);

б) (a + 8) + b;

в) (a + 7) + (b + 13);

г) (a – 5) + (b – 2);

д) (a + 9) + (b – 11);

е) (a – 6) + (b + 15)?

Ответ обоснуйте.

19. Познакомьтесь с правилами прибавления числа к сумме, суммы к числу, суммы к сумме. Какие законы сложения натуральных чисел лежат в основе этих правил?

20. Используя законы сложения, преобразуйте выражение
(3 + 2) + 7 к виду (3 + 7) + 2; а выражение (3 + 2) + (4 + 5) к виду
(3 + 4) + (2 + 5). Каждый шаг в преобразовании обоснуйте.

21. Вместо звездочки поставьте знак «=», «>» или «<», чтобы получилось истинное высказывание.

а) 4986 + 7367 * 4968 + 7370;

б) 2819 + 6885 * 2820 + 6734;

в) 71598 + 39 * 71600 + 36;

22. Объясните выбор действия, которым решаются задачи:

а) Саша поймал 4 рыбки, а Миша 3 рыбки. Сколько всего рыбок поймали дети?

б) Из коробки взяли 4 зеленых карандаша и 3 красных. Сколько карандашей взяли из коробки?

Какие теоретико-множественные понятия используются при решении этих задач.

23. Решите задачи различными способами, дайте обоснование.

а) В колхозе было 8 грузовых машин и 2 легковые. Колхоз купил еще 2 машины. Сколько всего машин стало в колхозе?

б) У малышей детского сада было 20 красных мячей и 10 зеленых. Им подарили еще 8 мячей. Сколько мячей стало у малышей?

Дата добавления: 2014-12-27