Неотрицательных чисел

Тема 5. Вычитание на множестве целых

Контрольные вопросы по теории

1. Сформулируйте определение операции вычитания целых неотрицательных чисел.

2. Дайте теоретико-множественное истолкование разности двух целых неотрицательных чисел.

3. Сформулируйте условие существования разности целых неотрицательных чисел и докажите его.

Практические задания

1. Пользуясь аксиоматическим определением вычитания, найдите значения выражений: а) 7 – 5; б) 3 – 3; в) 4 – 0.

2. Приведите примеры двух заданий из учебника по математике для начальных классов, при выполнении которых используется условие существования разности целых неотрицательных чисел.

3. Даны множества А = {1; 2; 3; 4; 5; 6; 7} и В = {1; 3}.

а) Найдите множество .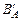

б) Изобразите при помощи кругов Эйлера множества А, В, .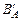

в) Истинно ли равенство 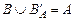? Почему?

г) Истинно ли равенство n (B) +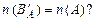

4. Объясните с теоретико-множественной точки зрения смысл равенств: а) 8 – 3 = 5; б) 4 – 4 = 0; в) 3 – 0 = 3.

5. Из учебников математики для начальных классов приведите примеры заданий, при выполнении которых используются:
а) определение разности через дополнение подмножества; б) определение разности через сумму.

6. Объясните, почему нижеприведенные задачи решаются при помощи вычитания:

а) У пруда росло 9 осин. 4 осины спилили. Сколько осин осталось у пруда?

б) Вова и Лида нарисовали 9 домиков. Лида нарисовала 4 домика. Сколько домиков нарисовал Вова?

7. Составьте задачу, в которой нужно найти число элементов дополнения одного множества до другого. Каким действием решается составленная задача? Почему?

8. Может ли разность целых неотрицательных чисел быть равной: а) уменьшаемому; б) вычитаемому; в) нулю? Что можно сказать о разности натуральных чисел?

9. Обладает ли операция вычитания целых неотрицательных чисел свойством коммутативности? Свойством ассоциативности?

10. Запишите, используя символы, правила связывающие сложение и вычитание. Дайте их теоретико-множественную трактовку. Приведите примеры использования этих правил в начальном курсе математики.

11. В учебнике по математике для начальной школы приведено правило: «Для проверки вычитания к разности прибавляют вычитаемое. Если решение правильное, то получится уменьшаемое». Каково теоретическое обоснование этого правила?

12. На основании зависимости между компонентами и результатом действия найдите множество целых неотрицательных корней уравнения:

а) 43 – х = 20;

б) 20 – х = 43;

в) х – 20 = 43;

г) х – 43 = 20.

13. Дайте теоретико-множественное истолкование правил:
а) вычитание числа из суммы; б) вычитание суммы из числа. Проиллюстрируйте их с помощью кругов Эйлера.

14. Какими способами можно найти разность:

а) 11– (3 + 1); б) (7 + 8) – 5?

15. Какие свойства вычитания являются теоретической основой следующих приемов вычислений, изучаемых в начальном курсе математики:

а) 48 – 30 = (40 +8) – 30 = 10 + 8 = 18;

б) 42 – 5 = 42 – (2 + 3) = 40 – 3 = 37.

16. Можно ли, не выполняя вычислений сказать, значения каких выражений будут равны:

а) 50 – (16 +14);

б) (50 – 16) + 14;

в) (50 – 16) –14;

г) (50 – 14) +16;

д) (50 – 14) –16;

е) 50 – 16 –1 4;

ж) (50 +16) –14;

з) 50 + (16 –14);

и) 50 – (16 –14);

к) 50 + 14 – 16.

17. Объясните, на основе каких теоретических положений можно выполнить следующие преобразования:

а) (7 + 5) – (3 + 4) = (7 – 3) + (5 – 4) = 4 + 1 = 5;

б) (7 + 5) – (3 + 4) = (7 – 4) + (5 – 3) = 3 + 2 =5.

18. Вычислите устно, давая обоснование примененных приемов:

а) (458 + 1257) – 657;

б) 878 + (122 –81);

в) (1459 –743) +343;

г) 2944 – (2523 – 1056);

д) 5331 – (597 + 4331);

е) (2583 – 694) – 1306;

ж) 657 –353 –257;

з) 1423 +889 –723;

и) 607 – 359;

к) 597 – 429.

19. Вычислить рациональным способом:

а) (37891 – 1576) + 1109;

б) 56877 – (6877 + 123);

в) 93785 + (4796 – 1685);

г) 65849 – (14849 – 3151);

д) 890693 – (70020 – 4653 + 3895);

е) (89765 + 10134 – 19867) – 38695.

20. Найдите в учебниках математики начальной школы упражнения, которые раскрывают изменение разности двух чисел в зависимости от изменения одного из компонентов этого действия.

21. Заполни таблицу:

	Уменьшаемое	Вычитаемое	Разность
1.	+ 12	+24	?
2.	–19	–39	?
3.	+32	–34	?
4.	–50	+17	?
5.	+22	?	–18
6.	–25	?	+34

22. Нижеприведенные задачи решите различными способами, дайте обоснования:

а) В одной банке было 10 соленых огурцов, а в другой 6 огурцов. За обедом съели 4 огурца. Сколько всего огурцов осталось?

б) В гараже стояло 20 машин, сначала выехало 7 машин, а потом 3 машины. Сколько машин осталось в гараже?

23. Запишите следующие предложения в виде равенства:

а) 810 больше 320 на 490; б) 319 меньше 536 на 217.

24. Выясните, с какими теоретико-множественными понятиями встречаются (в неявном виде) ученики 1 класса при решении следующих задач:

а) На одной полке 5 книг, на другой на 3 больше. Сколько книг на двух полках?

б) Во дворе гуляли 6 мальчиков, а девочек на 2 меньше. Сколько всего детей гуляло во дворе?

в) На столе 8 чашек, их на 3 больше, чем стаканов. Сколько стаканов на столе?

г) На верхней полке шкафа 7 книг, а на нижней 4. На сколько книг больше на верхней полке, чем на нижней?

25. Решите нижеприведенные задачи и объясните, чем отличаются их решения:

а) В одной бочке 40 ведер воды. Утром на поливку цветов израсходовали 12 ведер, а вечером10 ведер. Сколько ведер воды осталось в бочке?

б) В одной бочке было 40 ведер воды, а в другой 12 ведер. На поливку цветов израсходовали10 ведер. Сколько ведер воды осталось в бочках?

Дата добавления: 2014-12-27