Окружность и ее уравнение

Понятие кривой второго порядка

Лекция 7. КРИВЫЕ ВТОРОГО ПОРЯДКА.

План:

1. Понятие кривой второго порядка.
2. Окружность и ее уравнение.
3. Эллипс и его уравнение.
4. Гипербола и ее уравнение.
5. Парабола и ее уравнение.

Кривая второго порядка – линия на плоскости, задаваемая уравнением: Ах²+2Вху+Су²+2Dx+2Ey+F=0, где коэффициенты А, В, С, D, E, F – любые действительные числа при условии, что А, В, С одновременно не равны нулю.

Выделяют следующие кривые второго порядка:

· окружность;

· эллипс;

· гипербола;

· парабола.

Окружностью называется множество точек плоскости, равноудаленных от одной точки, называемой центром.

Пусть центром окружности является точка О (a;b), а расстояние до любой точки М (x;y) окружности равно R (рис. 7.1). Составим уравнение окружности.

Расстояние от точки М до центра окружности можно найти, пользуясь формулой расстояния между точками:

.

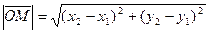Подставив в это выражение координаты точек М и О,получим:

Рис. 7.1

.

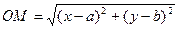Поскольку расстояние ОМ равно радиусу R, следовательно, .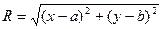

Возведём обе части уравнения в квадрат: .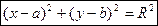

Это уравнение называется каноническим уравнением окружности с центром О (a; b) и радиусом R.

Если центр окружности совпадает с началом координат, то уравнение окружности имеет вид: x ² + y ²= R ².

Пример 7.1. Составьте уравнение окружности с центром О (3; -2) и радиусом r = 5.

Решение. Подставив a = 3, b = -2 и r = 5 в каноническое уравнение окружности 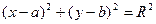, получим: .

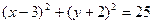Пример 7.2. Докажите, что линия, заданная уравнением х²+у²+6х-4у-3=0, является окружностью, найти координаты ее центра и радиуса.

Решение. Попытаемся привести уравнение линии к виду: 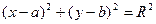. Для этого выделим в уравнении полные квадраты. Имеем (х²+6х)+(у²-4у)-3=0.

Для получения полного квадрата к первой скобке добавим 9, ко второй 4, и вычтем числа 9 и 4 соответственно: (х²+6х+9)-9+(у²-4у+4)-4-3=0.

Получим, что (х+3)²+(у-2)²-16=0 или (х+3)²+(у-2)²=16 – уравнение окружности с центром О (-3;2) и радиусом 4.

Ответ: О (-3;2), R =4.

Дата добавления: 2014-12-27