Операции над векторами в координатах

№	Вид операции	на плоскости	в пространстве
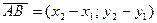
	Координаты вектора	А (х1; у1); В (х2;у2)	А (х1; у1; z1); В (х2; у2; z2)
	Длина вектора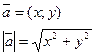
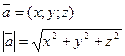
	Сложение и вычитание векторов	;	;
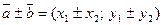
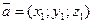	Умножение вектора на число	;	;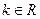
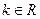
	Скалярное произведение векторов	;	;
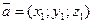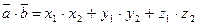
	Угол между векторами
	Координаты середины отрезка	А (х1; у1); В (х2;у2)	А (х1; у1; z1); В (х2; у2; z2)
	Расстояние между точками	А (х1; у1); В (х2;у2)	А (х1; у1; z1); В (х2; у2; z2)

Справедливы следующие теоремы:

Теорема 1. Если векторы и 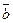коллинеарны, то их соответствующие координаты пропорциональны.

на плоскости	в пространстве
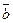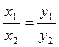Если = (х1; у1) и = (х2; у2) коллинеарны, то .	Если = (х1; у1; z1) и 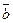= (х2; у2; z2) коллинеарны, то .

Теорема 2. Если ненулевые векторы и 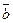взаимно перпендикулярны, то их скалярное произведение равно нулю, и наоборот, если скалярное произведение векторов равно нулю, то векторы перпендикулярны:

() .

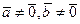Пример 5.1. Даны точки А (4;-3;1), В (-2;-9;3).

Найдите: 1) координаты вектора ;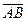

2) длину вектора ;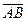

3) координаты точки М – середины АВ.

Решение:

1) Воспользуемся формулой нахождения координат вектора: .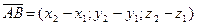

Тогда ; .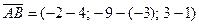

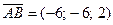2) Зная координаты вектора 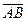, найдем его длину по формуле: .

.

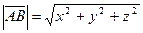3) Пусть точка М – середина отрезка АВ. Тогда ее координаты находятся по формуле: .

М ; М (1; -6; 2).

Ответ: 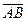=(-6; -6; 2), , М (1; -6; 2).

Пример 5.2. Даны , .

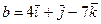Найдите: 1) ;

2) ;

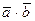3)

Решение:

1) Вектор задан в виде разложения по базисным векторам 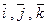. Его координаты находятся как коэффициенты разложения вектора по базису: .

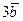Найдем координаты векторов и по формуле: . Тогда

= (6; 10; – 4); 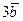= (12; 3; –21);

Воспользуемся формулой нахождения суммы и разности векторов: . Получим, что

= (6-12; 10-3; -4-(-21));

= (-6; 7; 17).

2) Воспользуемся формулой нахождения скалярного произведения векторов: .

Получим: ;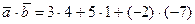

;

.

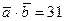3) Найдем косинус угла между векторами по формуле = .

=

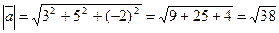
Ответ: 1) = (-6; 7; 17)

2)

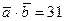
3) =

Пример 5.3. При каком значении n векторы ,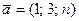

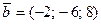
1) коллинеарны; 2) перпендикулярны?

Решение:

1) Воспользуемся теоремой 1: если векторы коллинеарны, то их соответствующие координаты пропорциональны. Получим, что

;

.

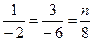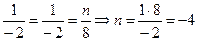Следовательно, при n = – 4 векторы и коллинеарны.

2) Воспользуемся теоремой 2: если

Þ –2 – 18 + 8 n = 0;

8 n = 20;

n = ;

n = 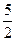; n = 2,5.

Следовательно, при n =2,5 векторы и перпендикулярны

Ответ: 1) n = – 4; 2) n = 2,5.

Контрольные вопросы:

1. Что называется вектором?
2. Какие виды векторов существуют?
3. Какие операции над векторами как над направленными отрезками можно выполнить?
4. Как задается скалярное произведение векторов?
5. Что называют линейной комбинацией векторов?
6. Что называют базисом на плоскости и в пространстве?
7. Какие векторы задают прямоугольную систему координат на плоскости и в пространстве?
8. Что называют координатами вектора?
9. Какие операции над векторами в координатах можно выполнять?
10. Каков признак коллинеарности векторов?
11. Сформулируйте признак перпендикулярности векторов.

Дата добавления: 2014-12-27