Формула трапеций

Задача численного интегрирования

ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Лекция 47. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ

План:

1. Задача численного интегрирования.

2. Формулы прямоугольников.

3. Формула трапеций.

4. Формула парабол (Симпсона).

Не для всякой функции можно вычислить определенный интеграл с помощью известных нам способов. Кроме того, на практике часто сталкиваются с функциями, заданными табличным и графическим способами, или с функциями, интегралы от которых выражаются через очень громоздкие функции. В этих случаях вычисления по формуле Ньютона-Лейбница либо невозможны, либо затруднительны, поэтому прибегают к различным методам приближенного (численного) интегрирования.

Рис. 47.1.

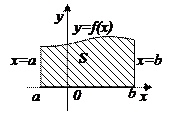Рассмотрим функцию , непрерывную на отрезке и для наглядности . Тогда в силу геометрического смысла определенного интеграла, он численно равен площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми х=а и х = b, отрезком [ a;b ] оси Ох, т.е. = S (рис. 47.1).

Основная задача методов численного интегрирования заключается в том, чтобы как можно точнее найти площадь фигуры S. Это число как раз и будет являться приближенным значением определенного интеграла.

2. 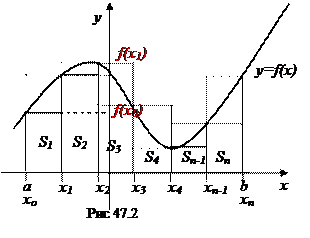Формулы прямоугольников

Попытаемся заменить криволинейную трапецию ступенчатой фигурой, состоящей из прямоугольников. Для этого выполним следующие действия (рис. 47.2).

1. С помощью точек х_о=а, х₁, х₂,…, х_п=b разобьём отрезок [ a;b ] на п равных частей. Тогда длина каждого отрезка будет равна 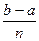. Её называют шагом разбиения и обозначают h.

2. На каждом отрезке [ х_о;х₁ ], [ х₁;х₂ ] … [ х_п-1;х_п ] построим прямоугольники высотой f (х ₀), f (х ₁), f (х ₂),…, f (х_п-1).

3. Найдем площадь каждого прямоугольника как произведение его длины на ширину:

; … .

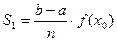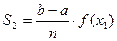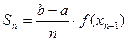Тогда сумма площадей всех прямоугольников S будет равна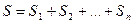

.

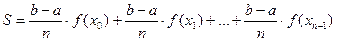Вынесем 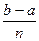за скобки: .

Поскольку сумма площадей всех прямоугольников S приближенно равна площади криволинейной трапеции, то можно считать, что

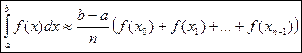(1) – формула прямоугольников.

Если в качестве высоты прямоугольников брать значения функции не в левом, а в правом конце отрезка (рис. 47.2), то формула прямоугольников будет иметь вид:

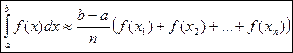(2) – формула прямоугольников.

Пример 47.1. Вычислите определенный интеграл :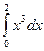

а) по формуле Ньютона-Лейбница;

б) по формулам прямоугольников (число точек деления п = 4).

Решение. а) 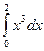= 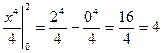- точное значение .

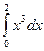б) Выпишем подынтегральную функцию 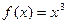и рассмотрим ее на отрезке [0; 2] (, 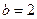). Поскольку число точек деления отрезка равно 4, найдем ширину каждого отрезка (шаг) по формуле : .

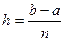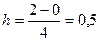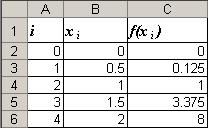
Для удобства вычислений все расчеты будем выполнять в электронных таблицах Microsoft Excel. В качестве шапки таблицы можно предложить следующий вариант:

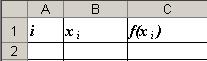
В столбце А будет указываться номер выполняемого шага: 0, 1, 2… п.

В столбце В будут располагаться значения х ₀, х ₁, х ₂ …. х_п. Поскольку х_о=а, то в ячейку В2 занесем значение 0. Чтобы найти значение х ₁, которое будет находиться в ячейке В3, достаточно к началу промежутка а прибавить ширину шага h. В ячейке В3 будет находиться число 0 + 0,5 = 0,5. Для нахождения каждого последующего значения х к предыдущему необходимо прибавлять ширину шага до тех пор, пока х_п не будет равно b.

В столбце С будут содержаться значения функции в точках х ₀, х ₁, х ₂ … х_п, необходимые для расчета значения определенного интеграла по формулам (1) и (2). Чтобы их получить достаточно ввести формулу в ячейку С2. В нашем примере она будет иметь вид: =B2^3. Для заполнения столбца оставшихся значений можно воспользоваться возможностями автозаполнения. Тогда таблица будет иметь вид:

Рассчитаем приближенное значение определенного интеграла по формуле прямоугольников (1) в ячейке D2, по формуле прямоугольников (2) в ячейке Е2. Множитель 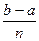нами уже вычислен, он равен 0,5, поэтому формулы в ячейках D2 и Е2 будут иметь вид:

D2: =0.5*СУММ(C2:C5) (поскольку суммируются значения функции, начиная с f (х ₀)и заканчивая f (х_п-1));

Е2: =0.5*СУММ(C3:C6)(суммируются значения функции, начиная с f(х ₁) и заканчивая f(х_п)).

Результирующая таблица будет следующей:

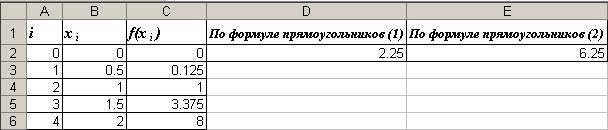Видим, что полученные по формулам прямоугольников значения определённого интеграла (2,25 и 6,25) достаточно сильно отличаются от его реального значения (4). Очевидно, что с увеличением числа точек деления приближенное значение определенного интеграла будет ближе к реальному. Но все равно метод прямоугольников относится к числу наименее точных. Рассмотрим другие методы численного интегрирования.

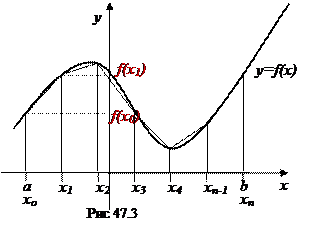Идея метода трапеций похожа на идею метода прямоугольников: попытаться заменить исходную криволинейную трапецию ступенчатой фигурой, состоящей из трапеций. Для этого выполним следующие действия (рис. 47.3).

1. С помощью точек х_о=а, х₁, х₂,…, х_п=b разобьём отрезок [ a;b ] на п равных частей длиной .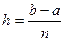

2. На каждом отрезке [ х_о;х₁ ], [ х₁;х₂ ] … [ х_п-1;х_п ] построим трапеции, соединив отрезками точки (х ₀; f (х ₀)) и (х ₁; f (х ₁)), (х ₁; f (х ₁)) и (х ₂; f (х ₂)),…, (х_{п -1}; f (х _{п -1})) и (х_п; f (х _п))

3. Найдем площадь каждой трапеции как произведение полусуммы её оснований на высоту. Длины оснований первой трапеции будут равны f (х ₀) и f (х ₁), а высота 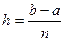. Тогда

.

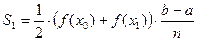Для второй трапеции длины оснований равны f (х ₁) и f (х ₂), а высота та же: 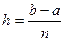. Тогда .

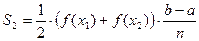Аналогично …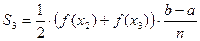

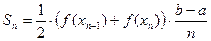
Найдем сумму площадей всех трапеций S: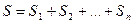

+ +…+ .

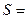
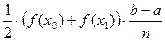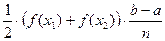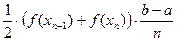Вынесем 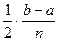за скобки: =

= =

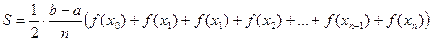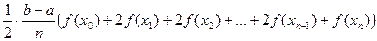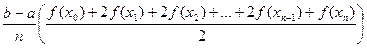= или

.

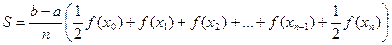Поскольку сумма площадей всех трапеций S приближенно равна площади криволинейной трапеции, то можно считать, что

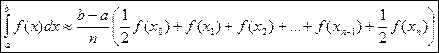(3)– формула трапеций.

Пример 47.2. Вычислите приближенное значение определенного интеграла 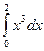по формуле трапеций (число точек деления п = 4).

Решение. Воспользуемся решением примера 47.1. Рассмотрим функцию 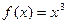на отрезке [0; 2], который разбит на четыре части шириной .

В уже созданной в Microsoft Excel таблице в ячейку D4 запишем формулу для расчета приближенного значения определенного интеграла 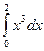по формуле трапеций (3).

Поскольку шаг равен 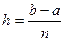=0,5, то его нужно умножить на скобку, содержащую полусумму первого и последнего значения функции и сумму всех остальных значений функции из столбца С. Тогда формула в ячейке D4 будет иметь вид: =0.5*((C2+C6)/2+СУММ(C3:C5)).

Расчетная таблица будет следующей:

Полученное по формуле трапеций значение определённого интеграла (4,25) ближе к реальному значению (4), чем значения, вычисленные по формулам прямоугольников. Рассмотрим последний метод – метод парабол - и оценим его точность.

Дата добавления: 2014-12-27