Метод Эйлера

Задача численного решения дифференциальных уравнений.

Напомним, что дифференциальным называется уравнение, содержащее производную или дифференциал искомой функции, например, 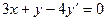. Подчеркнем, что решением дифференциального уравнения является не число, а функция. Причем дифференциальное уравнение имеет множество решений, которые можно изобразить в виде семейства интегральных кривых.

В практике чаше всего приходится иметь дело с задачей Коши: найти решение дифференциального уравнения при заданных начальных условиях (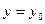 при 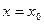). Геометрически это означает, что нужно выделить отдельную интегральную кривую, проходящую через точку .

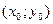Потребность в приближенном решении задачи Коши возникает прежде всего в том случае, если дифференциальное уравнение не принадлежит ни к одному из классов дифференциальных уравнений, для которых известны точные методы решения. Приближенные методы часто применяют и тогда, когда точные методы оказываются неэффективными, приводят к очень сложным расчетам и интегралам.

Пусть необходимо решить дифференциальное уравнение вида 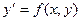при заданных начальных условиях ( 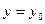при 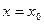) на отрезк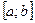е , где 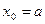. С помощью метода Эйлера мы сможем построить таблицу значений искомой функции у на отрезке 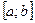вида:

X	хо=а	х1	х2	…	хп-1	хп=b
Y	уо	у1	у2	…	уп-1	уп

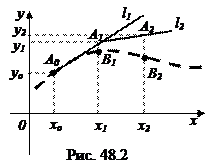Выполним следующие действия:

1. С помощью точек х_о=а, х₁, х₂,…, х_п=b разобьём отрезок 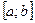на п равных частей длиной .

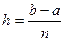2. Попытаемся искомую интегральную кривую приближенно заменить касательными, проведенными в крайней левой точке каждого отрезка [ х_о;х₁ ], [ х₁;х₂ ] … [ х_п-1;х_п ] (рис. 48.2) – А ₀ А ₁, А ₁ А ₂…

Уравнение касательной, проведенной к графику функции 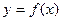в точке 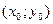, имеет вид: (*).

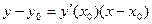3. Рассмотрим первый отрезок [ х_о;х₁ ]. Касательная l ₁, которую мы проводим к графику искомой функции в точке А ₀, должна пройти через известную точку А ₀ 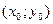и через некоторую точку А ₁ 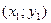, абсцисса которой – известное значение х₁, а ордината неизвестна.

Поскольку точк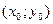и и 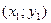лежат на касательной l ₁, их координаты удовлетворяют уравнению касательной (*): .

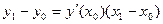По условию исходное дифференциальное уравнение имеет вид 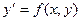, отсюда .

Подставим 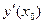в уравнение касательной l ₁: .

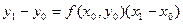Длина отрезка [ х_о;х₁ ] равна 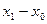или 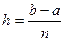, следовательно, уравнение касательной l ₁ примет вид: .

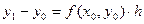Выразим из этого уравнения неизвестную переменную : 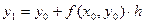(1).

С помощью формулы (1) мы нашли ординату точки А ₁, лежащей на касательной l ₁. Если выбирать длину отрезка [ х_о;х₁ ] по-возможности небольшой, то ордината точки В ₁, лежащей на искомой интегральной кривой и имеющей ту же абсциссу 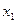, будет мало чем отличаться от найденного значения .

4. Рассмотрим отрезок [ х₁;х₂ ]. Координаты точки А ₁ 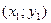нам известны, необходимо найти ординату 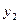точки А ₂ 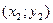. Проведя ту же цепочку рассуждений, что и в пункте 3, найдем формулу для расчета 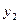: 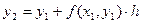(2).

Полученное число 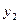будем считать приближенным значением искомой функции в точке .

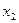Формулу (2) в общем виде можно записать следующим образом: 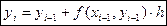, где 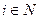, , 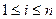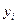- значения искомой функции в точках 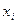. Для удобства все найденные значения 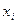и 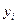заносят в таблицу.

Пример 48.1. Дано дифференциальное уравнение 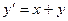. Найдите методом Эйлера на отрезке 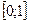с шагом численное решение задачи Коши с начальным условием .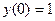

Решение. Заданное дифференциальное уравнение 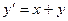соответствует виду дифференциальных уравнений 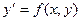, для которых применим метод Эйлера. В нашем случае .

Для удобства вычислений все расчеты будем выполнять в электронных таблицах Microsoft Excel. В качестве шапки таблицы можно предложить следующий вариант:

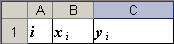
В столбце А будет указываться номер выполняемого шага: 0, 1, 2… п.

В столбце В будут располагаться значения х ₀, х ₁, х ₂ …. х_п. Поскольку х_о – начало отрезка 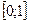, то в ячейку В2 занесем значение 0. Чтобы найти значение х ₁, которое будет находиться в ячейке В3, достаточно к началу промежутка х ₀ прибавить ширину шага h. В ячейке В3 будет находиться число 0 + 0,1 = 0,1. Для нахождения каждого последующего значения х_i к предыдущему необходимо прибавлять ширину шага до тех пор, пока х_п не будет равно концу отрезка (числу 1).

В столбце С будут содержаться значения искомой функции в точках х ₀, х ₁, х ₂ … х_п. Значение 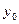берем из условия задачи Коши: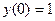 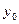=1. Заносим это число в ячейку С2. Чтобы получить значение , в ячейку С3 достаточно ввести формулу, аналогичную формуле (1). В нашем примере она будет иметь вид: =C2+(B2+C2)*0.1. Для заполнения столбца оставшихся значений 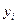можно воспользоваться возможностями автозаполнения. Тогда расчетная таблица будет иметь вид:

Рис. 48.3

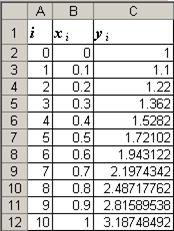
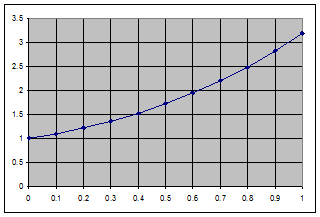
Данная таблица как раз и представляет собой численное решение задачи Коши методом Эйлера. Пользуясь этой таблицей можно построить на отрезке 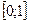искомую интегральную кривую, проходящую через точку (0; 1) (рис 48.3).

Подведем итог. Метод Эйлера задает простой алгоритм вычислений, но определяет табличные значения 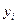с небольшой степенью точности. Это связано с тем, что касательная проводится в левом конце каждого рассматриваемого отрезка, и не учитывается поведение интегральной кривой на всем отрезке. По этой причине приближения 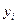оказываются достаточно грубыми, причем расхождения 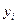с истинными значениями искомой функции растут к концу таблицы. Существуют другие, более точные методы решения задачи Коши – метод Эйлера-Коши и метод серединных точек (см. Исаков В.Н. "Элементы численных методов", глава 5, §5.4).

Контрольные вопросы:

1. В чем заключается сущность задачи Коши при решении дифференциальных уравнений?

2. Когда применяются методы численного решения дифференциальных уравнений?

3. В чем заключается сущность метода Эйлера?

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Александрова Н.В. Математические термины: справочник / Н.В. Александрова. - М.: Высш. школа, 1978. - 190 с.

2. Валуце И.И. Математика для техникумов на базе средней школы: Учеб. пособие / И.И. Валуце, Г.Д. Дилигул. – М.: Наука, 1989. – 576 с.

3. Вычислительная математика: Учебное пособие для техникумов /Н.И.Данилина [и др.]; - М.: Высш. шк., 1985. – 372 с.

4. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2004. – 320с.

5. Исаков В.Н. Элементы численных методов: учеб. пособие для студ. высш. пед. учеб. заведений / В.Н. Исаков. – М.: Издательский центр "Академия", 2003. – 192 с.

6. Курс высшей математики для гуманитарных специальностей: Учеб. пособие / Ю.Д.Максимов [и др.]; - СПб.: Специальная Литература, 1999. – 191 с.

7. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с.

8. Математика для техникумов. Алгебра и начала анализа: Учебник. Ч. 2. / под ред. Г.Н.Яковлева. – 3-е изд. – М.: Наука, 1988. – 272 с.

9. Письменный Д.Т. Конспект лекций по высшей математике: [в 2 ч.] Ч.2. / Д.Т. Письменный. – М.: Айрис-пресс, 2007.- 256 с.

10. Сборник задач по дифференциальным уравнениям и вариационному исчислению / В.К.Романко [и др.]; - М.: ЮНИМЕДИАСТАЙЛ, 2002. – 256 с.

11. Энциклопедия для детей. Т.11. Математика / Глав. ред. М.В.Аксенова. - М.: Аванта+, 2000. - 688 с.

Дата добавления: 2014-12-27