Метод хорд

Пусть необходимо найти корень уравнения вида 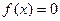с точностью ε, если известно, что корень принадлежит промежутку [ а; b ]. Графически это означает, что необходимо найти нули функции – значения переменной х, в которых график пересекает ось Ох, и эти значения по условию должны принадлежать промежутку [ а; b ].

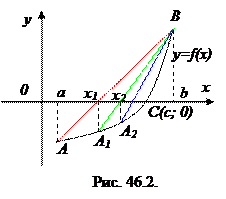
Рассмотрим функцию 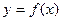на отрезке [ а; b ] (рис. 46.2). График данной функции обязательно пересекает ось Ох в некоторой точке С (с; 0). Наша задача – найти абсциссу этой точки – значение с.

Выполним следующие действия:

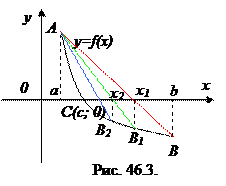
1. Проведем хорду АВ. Она пересекает ось Ох в точке с абсциссой х ₁.

2. Выберем точку на кривой, абсцисса которой равна х ₁ – точка А ₁.

3. Проведем хорду А ₁ В. Она пересекает ось Ох в точке с абсциссой х ₂.

4. Выберем точку на кривой, абсцисса которой равна х ₂ – точка А ₂ и т.д.

Будем продолжать этот процесс до тех пор, пока разность между последующим х_{п +1} и предыдущим х_п значениями переменной х не станет меньше заданной в условии задачи точности ε, т.е. 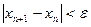. Это означает, что х_{п +1,} х_п практически не будут отличаться от с.

Выведем формулы для нахождения х ₁, х ₂… х_{п +1}:

1. Выпишем координаты точек А и В: , .

2. Составим уравнение прямой АВ: .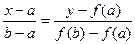

3. Найдем точку пересечения прямой АВ с осью Ох. Она имеет координаты (х ₁; 0). Заменим в уравнении АВ х на х ₁, у на 0: .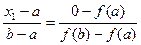

Выразим х ₁. По свойству пропорции .

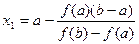4. Поскольку для нахождения х ₂ нужно проводить новую прямую через точк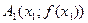и и и находить точку ее пересечения с осью Ох, произведем по аналогии следующую замену: роль а будет выполнять х ₁, роль х ₁ - х ₂. Получим, что .

5. Обобщим проведенные рассуждения. Для нахождения х_{п +1} будем использовать следующую формулу: 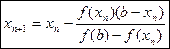(1).

В рассмотренном нами случае при проводимых преобразованиях точка В оставалась неподвижной.

Возможен и другой вариант: неподвижной может быть точка А (рис. 46.3). В этом случае будем использовать другую формулу: 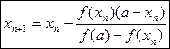(2).

Для удобства формулы (1) и (2) можно объединить в одну: 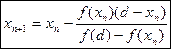(3), где d – абсцисса неподвижной точк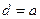и ( или 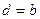), 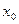- конец отрезка [ а; b ], не являющийся абсциссой неподвижной точки,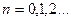

Правило выбора неподвижной точки:

Неподвижной точкой является тот конец отрезка [ а; b ], для которого знак функции в этой точке совпадает со знаком второй производной функции в той же точке.

Пример 46.2. Найти приближенное решение уравнения 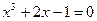на [0; 1], использую метод хорд с точностью ε = 0,01.

Решение. Составим функцию .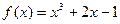

1. Выберем неподвижную точку. Для этого найдем и :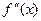

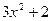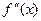= ; = 6 х. Найдем знак функции и второй производной на каждом конце отрезка: в точках 0 и 1.

; .

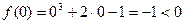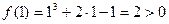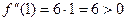; . Видим, что при 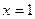знак функции совпадает со знаком второй производной. Следовательно, - абсцисса неподвижной точки.

2. Поскольку при решении задачи расчеты получаются достаточно громоздкие, их удобно выполнять с использованием компьютера, например, программы Microsoft Excel.

В качестве шапки таблицы можно предложить следующий вариант:

В столбце А будет указываться номер выполняемого шага п. Первое значение п всегда выбираем равным 0.

В столбце В будут располагаться значения х ₀, х ₁, х ₂ и т.д. В качестве х ₀ в ячейку В2 занесем значение того конца отрезка, который не является абсциссой неподвижной точки. В нашем случае это .

В столбце С будут содержаться значения функции в точках х ₀, х ₁, х ₂ и т.д., необходимые для расчета х_п+1 по формуле (3). Для нахождения f (х ₀) в ячейку С2 введем формулу. Поскольку 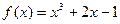, а первое значение х ₀ находится в ячейке В2, то формула будет иметь вид: =B2^3+2*B2-1.

В столбце D будет осуществляться проверка того, не превосходит ли 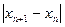заданной точности ε. Эта проверка будет начинаться с 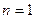, и ячейка D2 не заполняется.

Столбцы E и F – вспомогательные. Поскольку в формуле (3) используется d и f(d), то их можно один раз записать соответственно в ячейках E2 иF2 и в дальнейшем делать на них абсолютные ссылки.

После заполнения второй строки, она будет иметь вид:

Начнем заполнение третьей строки. Номер шага в ячейке А3 будет равен 1.

Для расчета х ₁ в ячейке В3 применим формулу (3), которая в программе Microsoft Excel примет вид: =B2-(C2*($E$2-B2))/($F$2-C2). Ссылки на ячейки E2 иF2 содержат знак "$", т.е. являются абсолютными, и при копировании данной формулы меняться не будут.

Для расчета f (х ₁) в ячейке С3 достаточно просто скопировать формулу из ячейки С2, и она будет иметь вид: =B3^3+2*B3-1.

В ячейку D3 занесем формулу для расчета модуля разности между последующим и предыдущим значением х: =ABS(B3-B2). Произведем проверку: если содержимое этой ячейки больше ε, то расчеты необходимо продолжить, меньше – закончить.

После заполнения третьей строки, она будет иметь вид:

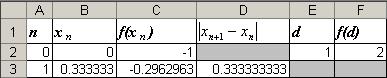
Достоинства программы Microsoft Excel с том, что нам достаточно ввести только формулы, все расчеты машина произведет сама. Видим, что содержимое ячейки D3=0,(3) больше заданной точности ε = 0,01, следовательно, расчеты следует продолжить.

Все основные формулы уже введены, в дальнейшем будем использовать только возможности автозаполнения. После выполнения следующих шагов таблица будет иметь вид:

Видим, что в ячейке D6 содержимое 0,006932015 стало меньше заданной точности ε = 0,01, следовательно, расчеты следует закончить и в качестве приближенного решения уравнения взять последнее х_п с точностью 2 знака после запятой. В нашем примере это х₄ 0, 45.

Ответ: х 0, 45.

Дата добавления: 2014-12-27