Лекция 48. Численное решение обыкновенных дифференциальных уравнений методом Эйлера

Формула парабол (Симпсона)

Если заменить график функции 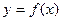не отрезками прямых, как в методах прямоугольников и трапеций, а дугами парабол, то получим более точною формулу вычисления интеграла .

Для использования метода Симпсона число точек деления должно быть четным. Тогда представим 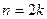. Приведем формулу парабол без вывода:

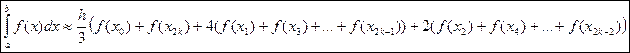(4) – формула парабол (Симпсона), где 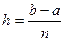- ширина шага.

Рассмотрим применение данного метода на конкретном примере.

Пример 47.3. Вычислите приближенное значение определенного интеграла 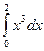по формуле парабол (число точек деления п = 4).

Решение. Воспользуемся решением примера 47.1. Рассмотрим функцию 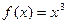на отрезке [0; 2], который разбит на четыре части шириной .

В уже созданной в Microsoft Excel таблице в ячейку Е4 запишем формулу для расчета приближенного значения определенного интеграла 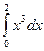по формуле парабол (4).

Перед скобкой должен стоять множитель . В нашем случае он будет равен 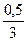. Выражение в скобках представляет собой сумму

· первого и последнего значения функции,

· умноженную на 4 сумму значений функций, имеющих нечетный индекс i,

· умноженную на 2 сумму значений функций, имеющих четный индекс i (за исключением i = п).

Тогда формула в ячейке Е4 будет иметь вид: =0.5/3*(C2+C6+4*(C3+C5)+2*C4).

Расчетная таблица будет следующей:

Видим, что приближенное значение определенного интеграла, вычисленное по формуле парабол (4) в данном примере совпадает с точным значением, вычисленным по формуле Ньютона-Лейбница. Из трех рассмотренных нами формул формула парабол дает лучшее приближение определенного интеграла , чем формулы прямоугольников и трапеций.

Контрольные вопросы:

1. В чем заключается геометрический смысл определенного интеграла?

2. Какова основная задача численного интегрирования?

3. В чем заключается сущность метода прямоугольников?

4. В чем заключается сущность метода трапеций?

5. В чем заключается сущность метода парабол?

6. Какой из методов численного интегрирования является наименее точным? Наиболее точным?

План:

1. Задача численного решения дифференциальных уравнений.

2. Метод Эйлера.

Дата добавления: 2014-12-27