Покращена версія моделі: врахування рівня комунікабельності мешканців

Усе

Усе

Відповідно в таблиці

комірка	формула
B3	= ЕСЛИ(C2*$E$3>=$E$4;$E$4-C2;C2*$E$3)

– п. 4.3:

якщо N_{j- 1} + D N не менше S

то в наступному рядку виконати присвоювання

N_j = S

інакше N_j = N_{j- 1} + D N

У таблиці це реалізувати наступною формулою:

комірка	формула
С3	= ЕСЛИ(B3=0;$E$4;C2 + B3)

Не забудьте (!) скопіювати формули з В3 і С3 в інші комірки в своїх стовпцях.

Перегляд нової таблиці (рис. 3.2) показує, що поставленої мети досягнуто: тепер досить одного погляду, щоб відразу встановити, після якого сеансу передавання все населення стає інформованим.

	A	B	C	D	E
	j	D N	N	Дано:
				N 0=
				K =
				S =
...	...	...	...

Рис. 3.2.

Прокоментуйте:

1) уміст виділених комірок таблиці (В10, В11, В12);

2) криву для D N, використовуючи дані цієї таблиці зі стовпців В і С, а також графік N = N (j);

3) «горбки» на графіку для D N при j = 10 і на графіку для N при j = 9 (а). Як позбутися цих «горбків» й отримати рис. 3.3(б)?

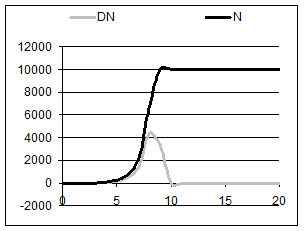
Рис. 3.3(а).

Рис. 3.3(б).

Висновки

1. Розглянута версія моделі є дуже спрощеною. Покладені в її основу Припущення 1-5 призводять до результату, який неважко
було б передбачити заздалегідь і без моделювання. А саме: чисельність знавців у міру зростання кількості передавань швидко й необмежено зростає.

2. Поява обмеження чисельності знавців принципово не робить модель більш достовірною. Ясно, що вжиті для цього заходи мають відверто штучний характер: обмеження кількості знавців жодним чином не випливає із самої моделі (із системи рівнянь).

3. На цьому етапі роботи ми не повинні серйозно обговорювати питання про відповідність між моделлю і даним процесом, тобто
питання про адекватність моделі: якщо вона й існує, то є слабкою.

Зауваження. При обговоренні питання про адекватність математичної моделі слід мати на увазі не адекватність взагалі (такої просто не існує), а адекватність стосовно певних ознак або властивостей об’єкту.

4. Основне значення цієї версії полягає в тому, що вона може
слугувати основою для подальшого поліпшення моделі.

5. Згідно п. 1 обчислювального експерименту вираз (3)

N_j = N_{j- 1}(1+ k)

задає геометричну прогресію, суму її перших j елементів можна знайти за відомою формулою. Якою?

Існує чимало об’єктів, що описуються цією формулою точно, проте вони ніяк не стосуються поширення чуток. Зокрема, якщо
N ₀ – розмір початкового грошового вкладу, а k – річний банківський відсоток, то S_j – розмір вкладу через j років. В даному прикладі j – обов’язково натуральне число. У ряді інших випадків j може набувати дійсних значень.

Спробуйте навести подібний приклад

Припущення, використані нами в попередній версії, були занадто простими, тому й результати роботи з моделлю практично виявилися нецікавими. Перейдемо до удосконалення моделі.

Згідно з Припущенням 4 наша модель передбачає однорідний за ознакою балакучості склад населення. У житті такого зазвичай не буває. Тому, в першу чергу, частково знімемо це обмеження і сформулюємо

Припущення 4*. Вважатимемо, що населення складається з трьох груп: звичайних людей з параметром передавання k_зв, балакунів з
параметром передавання k_б (k_б>k_зв) і мовчунів з параметром передавання k_м = 0. При цьому, як і раніше, значення названих параметрів вважатимемо незмінними в часі.

Нехай доля мовчунів складає M, а балакунів – B від усієї кількості мешканців. Тоді доля Z звичайних знавців складатиме

Z = 1 – M – B.

Не повинно викликати серйозних заперечень твердження, що при досить великій чисельності населення так само розподіляються відповідні частки і серед знавців новини. Так, наприклад, якщо доля мовчунів серед усього населення складає М, то й серед знавців ця доля також буде М.

Тепер приріст Δ N кількості знавців після j -го сеансу передавання забезпечуватиметься балакунами і звичайними оповідачами:

Δ N = N_{j– 1} ·B·k_б + N_{j– 1} ·k_зв· (1 – M – B) (4)

за рахунок за рахунок

балакунів звичайних

або

Δ N = N_{j– 1} · (B·k_б + k_зв·Z); (5)

загальну ж кількість знавців будемо шукати згідно (2):

N_j = N_{j– 1} + Δ N

або з урахуванням (5)

N_j = N_{j– 1}(1+ B·k_б+ k_зв·Z)(5*)

Рівняння(5) і (2) або (5) і (5*) є поліпшеною математичною
моделлю процесу.

Модифікована таблиця має такий вигляд:

	A	B	C	D	E
	j	Δ N	N	Дано:
				M =
				B =
				kб =
				kзв =
				N 0 =
...	...	...	...

У відповідності з новими рівняннями потребує певних змін і

Дата добавления: 2015-01-03