Приклади розв’язання задач

Приклад 1. Два точкові електричні заряди 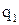= – 1 нКл і 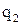=2 нКл знаходяться в повітрі на відстані r = 10 см один від одного. Визначити напруженість 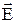у точці, яка знаходиться на відстані 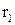= 9 см від першого заряду і 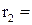7 см від другого.

Розв’язання.

Згідно принципу суперпозиції полів (3.4) напруженість поля може бути визначена як геометрична сума напруженостей полів 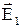і 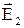кожного із зарядів: .

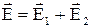Напруженість електричного поля, створеного у повітрі (ε =1) зарядом 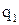дорівнює . (1)

Відповідно, 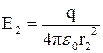. (2)

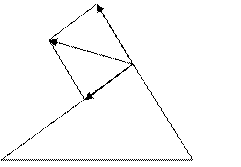
Вектор 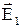спрямований вздовж радіальної прямої до заряду 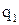, оскільки він негативний; відповідно, вектор 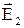спрямований від заряду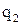

Рис. 3.1. (рис. 3.1). Абсолютне значення вектора

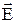знаходимо за теоремою косинусів:

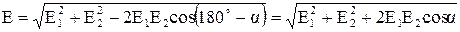, (3)

де α – кут між векторами 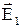і 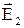. Його можна визначити з трикутника із сторонами r, 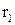і 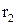. У даному випадку для спрощення зручно обчислити 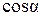окремо:

.

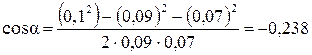Підставляємо вирази для 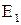і з формул (1) та (2) у формулу (3) й виносимо загальний множник за 1/4π 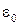за знак кореня.

.

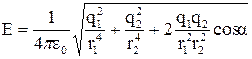Перевіряємо одиницю вимірювання:

.

Підставляємо числові значення в отриману формулу і проводимо обчислення з урахуванням значення 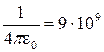м/Ф.

.

При обчисленні Е знак „–” заряду 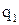пропущений, оскільки він визначає напрямок вектора напруженості, а цей напрямок був врахований при графічному зображенні.

Відповідь: Е = 3,56 кВ/м.

Примітка. Якщо відстань між зарядами та відстані між зарядами й точкою поля, в якій визначається напруженість, задані числами 3, 4, 5 (у будь-якій послідовності), або кратними ним, то трикутник – прямокутний. В цьому випадку замість теореми косинусів можна скористатися теоремою Піфагора.

Приклад 2. За умовами попередньої задачі визначити потенціал φ електричного поля зарядів 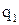і .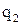

Розв’язання.

Згідно з принципом суперпозиції полів (3.15), потенціал φ сумарного поля, створеного зарядами 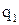і 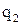, дорівнює алгебраїчній сумі потенціалів 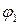і 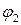полів, які створюються кожним з зарядів окремо

.

Потенціал електричного поля, яке утворюється у вакуумі точковим зарядом q на відстані r від нього (3.13)

.

Тоді .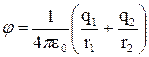

Перевірка одиниці вимірювання:

.

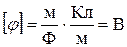Підставляємо в отриману формулу числові значення величин:

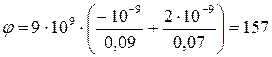
Відповідь: 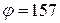В.

Приклад 3. Електричне поле створене позитивно зарядженою нескінченною ниткою. Рухаючись під дією поля від точки, що знаходиться на відстані r 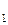= 1 см від нитки, до точки 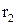= 4 см протон змінив свою швидкість від 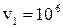м/с до 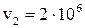м/с. Визначити лінійну густину заряду нитки.

Розв’язання.

Зміна кінетичної енергії протона 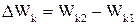пов’язана з роботою А сил електростатичного поля нитки:

. (1)

Поле нитки не є однорідним, тому роботу сил поля визначаємо шляхом інтегрування виразу для елементарної роботи

,

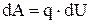де dU = – – різниця потенціалів між точками радіальної прямої, які знаходяться на відстані dr одна від одної. Напруженість Е поля нескінченної рівномірно зарядженої нитки визначається формулою

.

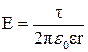Отже .

Звідки, з урахуванням теореми про кінетичну енергію (1), отримуємо

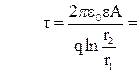
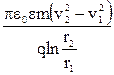. (2)

Перевіряємо одиницю вимірювання:

.

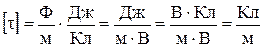Підставимо у формулу (2) числові значення.

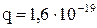Маса протона m = кг; заряд протона Кл; електрична стала ε 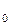= 8,85 10 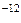Ф/м; ε=1.

Відповідь: τ=0,63 мкКл/м.

Приклад 4. Визначити силу струму I у провіднику, якщо за кожну секунду t = 1c через його переріз проходить N = 2 ·10¹⁷ електронів.

Розв’язання.

За визначенням (3.31) сила струму дорівнює заряду, який проходить через переріз провідника за одиницю часу. Кожен електрон переносить заряд q, тому за 1с всі вони перенесуть заряд N·q.

Тоді сила струму

I = ;

Перевіримо одиницю вимірювання.

[I] = 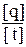= = 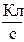A

Підставимо числові значення, знайшовши в таблицях заряд електрону q = 1,6·10^-19 Кл:

I = 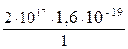= 3,2·10^-2 = 0,032 A.

Відповідь: I = 0,032 А.

Приклад 5. Сила струму у провіднику змінюється за законом

I = 2+2t, де I вимірюється в амперах, t – в секундах. Знайти заряд q, який проходить через переріз провідника за проміжок часу від t₁ = 1с до t₂ = 3с.

Розв’язання.

Відповідно до формули (3.31) можна записати: dq = Idt, тому для визна-чення повного заряду q треба здійснити інтегрування.

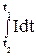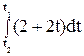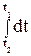q = = = 2 +2 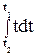= 2(t₂-t₁) + ( 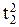- 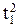) = 2(3-1) + (9-1) = =12Кл.

Відповідь: q = 12 Кл.

Приклад 6. Елемент з електрорушійною силою ε = 12 В при підключенні до зовнішнього опору R = 15 Ом дає струм I = 0,75 А. Визначити максимальний струм I_max (струм короткого замикання), який може дати цей елемент.

Розв’язок.

Застосуємо закон Ома для повного кола (3.36):

I = 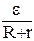, (1)

де ε – електрорушійна сила елемента; R – зовнішній опір; r – внутрішній опір елемента.

З формули (1) виразимо внутрішній опір r:

I (R + r) = ε;

IR + Ir = ε;

r = 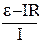. (2)

Максимальним струм у колі буде тоді, коли R = 0.

Тому

I_max = 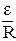(3)

Підставимо (2) в рівняння (3):

I_max = .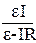

Перевіримо одиницю вимірювання.

[I_max] = 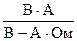= = 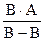A

Підставимо числові значення:

I_max = 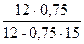= 12 А.

Відповідь: I_max = 12 А.

Дата добавления: 2015-01-03