Тема № 2

.

.

Для визначення 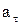і 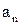зображуємо швидкість і прискорення м’яча в даній точці траєкторії і розкладаємо вектори на складові (рис. 1.3). З трикутників, утворених векторами швидкості, прискорення з їх складовими, випливає:

, ,

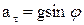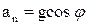де ;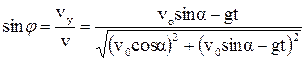

= .

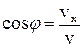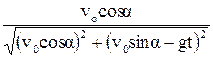Підставляємо числові дані і проводимо обчислення.

Н= 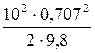м = 2,55 м; 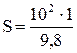м =10,2 м;

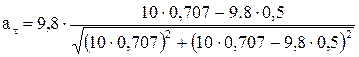м/с 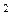= 2,87 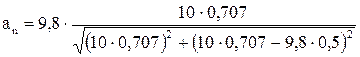м/с ;

м/с = 9,36 м/с .

Відповідь: Н = 2,55 м; 10,2 м; 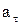= 2,87 м/с 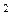; 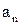= 9,36 м/с .

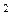Приклад 3. Велосипедист повинен проїхати по замкненій петлі радіуса R = 3 м. З якої висоти він може скотитися, щоб не впасти? Тертям знехтувати.

Розв’язання.

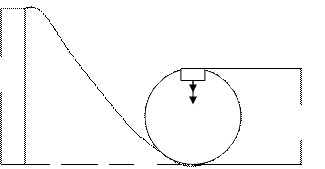
На тіло в верхній точці петлі діють дві сили, спрямовані вертикально вниз: сила тяжіння 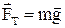и реакція опори 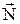. (Рис. 1.4). Вони надають тілу нормальне (доцентрове)

Рис. 1.4. прискорення (1.8):

.

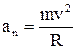За другим законом Ньютона (1.42)

.

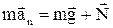У проекції на напрямок прискорення, з урахуванням виразу для нього, отримуємо .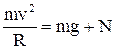

Таким чином, щоб не впасти велосипедист повинен мати швидкість, при якій задовольняється умова

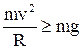, або .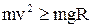

Необхідну швидкість велосипедист набуває, скотившись із гірки висотою Н. За законом збереження механічної енергії (1.81) його повна енергія 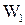на початку руху дорівнює повній енергії 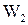у верхній точці петлі.

; .

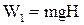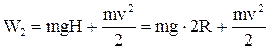З попередньої нерівності отримуємо

Звідки .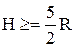

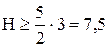м.

Відповідь: 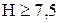м.

Приклад 4. Порожиста сталева кулька підіймається з глибини води h = 400 м на поверхню. Швидкість установленого руху кульки v´ = 1,2 м/с. На яку відстань і в якому напрямі відхилиться кулька? Широта місцевості φ= 60°.

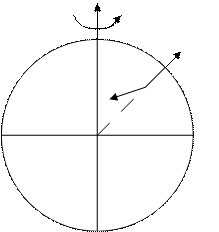Розв’язання.

Рух кульки розглядатимемо у системі відліку, яка зв’язана із Землею. На кульку діють чотири сили: гравітаційна 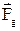, відцентрова 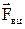, виштовхуюча (архімедова) 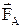та коріолісова 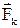. Векторна сума перших трьох сил визначає рух по вертикалі для заданого місця Землі. За умовою їх рівнодіюча дорівнює нулю, внаслідок чого рух кульки по вертикалі – рівномірний.

Сила Коріоліса (1.65)

Рис.1.5.

перпендикулярна до площини, в якій лежать вектори і 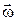, її напрямок визначається за правилом правого гвинта. В даному випадку вона перпендикулярна до площини рисунка і напрямлена на нас (рис. 1.5).

,

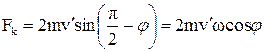де v´– швидкість, з якою кулька рухається відносно Землі; 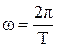– кутова швидкість обертання Землі; період обертання Т = 24 год. = 8,64· 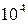с; 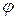– широта місцевості.

Сила 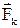надає кульці в горизонтальному напрямі на захід постійне прискорення .

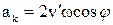За формулою шляху при рівноприскореному русі (1.19) знаходимо, що зміщення на захід кульки за час підйому 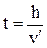дорівнює

Перевіряємо одиницю вимірювання

.

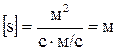Підставляємо значення величин у формулу

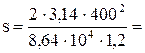9,69

Відповідь: s = 9,69 м.

Приклад 5. На спокійній воді озера стоїть човен довжиною L= 3м і масою M= 180 кг. На кормі човна стоїть людина масою m = 60 кг. На яку відстань s відносно берега переміститься човен, якщо людина перейде з корми на ніс човна?

Розв’язання.

Задачу вирішуємо у системі відліку, пов'язаною з берегом.

Припустимо для простоти, що людина йде відносно човна з постійною швидкістю 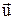. Тоді й човен буде рухатися рівномірно, і його переміщення s відносно берега дорівнює

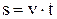, (1)

де v – швидкість човна відносно берега, t – час руху людини й човна.

За законом збереження імпульсу (1.67), оскільки на початку човен – нерухомий,

,

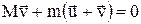де 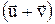- швидкість людини відносно берега.

У проекції на напрямок руху людини останнє рівняння має вид:

.

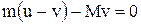Звідки для швидкості човна отримуємо

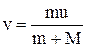. (2)

Час руху човна дорівнює часу руху людини вздовж човна, тобто

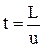. (3)

Підставляємо отримані для v і t вирази (2) та (3) у формулу (1) і знаходимо переміщення човна.

.

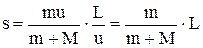Підставляємо в отриману формулу числові значення й обчислюємо s.

s = 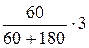м = 0,75 м.

Відповідь: s = 0,75 м.

Приклад 6. Блок масою m = 1 кг закріплений наприкінці столу. Гирі однакової маси 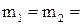1 кг з’єднані ниткою, яка перекинута через блок. Коефіцієнт тертя гирі 2 о стіл 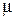=0,1. Визначити прискорення а, з яким рухаються гирі. Блок вважати однорідним диском. Тертям у блоці та вагою нитки знехтувати.

Розв’язання.

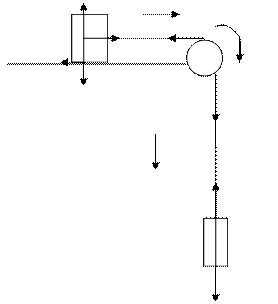
Розглянемо рух тіл, що входять у систему та сили, які діють на них. Тіла 1 і 2 рухаються поступально, тіло 1 – вниз, тіло 2 – вправо. Блок обертається відносно горизонтальної осі, що проходить через точку О. На тіло 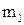діє сила тяжіння 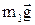і сила натягу нитки 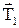. На тіло 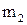– сила тяжіння 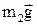, сила натягу нитки 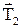, сила тертя 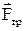та сила реакції опору 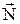. На блок – сили натягу нитки 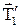і 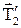. (Рис. 1.6.)

Рис. 1.6

Згідно ІІІ закону Ньютона = – , = – .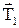

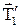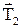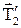Кутове прискорення ε, з яким рухається блок, пов’язано з лінійним прискоренням а співвідношенням (1.38)

.

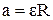Момент інерції блока, який має форму диска 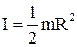(1.53). Сила тертя 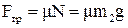(1.46).

На підставі ІІ закону Ньютона (1.42) записуємо рівняння руху тіл 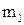і 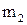в проекції на напрямок руху. Рух блоку описує основне рівняння динаміки обертального руху (1.69), який записуємо у проекції на ось О

;

;

;

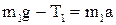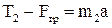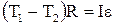Після підстановки ε та І, з урахуванням виразу для сили тертя, отримуємо

;

;

.

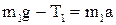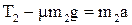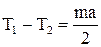Додаємо рівняння, що утворюють систему, один до одного і знаходимо прискорення

.

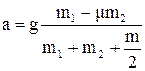Підставляємо числові дані

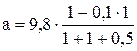м/с 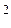=3,53 м/с .

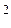Відповідь: а = 3,53 м/с .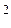

Приклад 7. В посудині з гліцерином падає свинцева кулька. Визначити максимальне значення діаметра кульки, при якому рух шарів гліцерину, спричинений рухом кульки, залишається ламінарним. В’язкість гліцерину η=1,0 Па·с.

Розв’язання.

Характер руху шарів рідини, який виникає завдяки силам внутрішнього тертя внаслідок руху тіла, визначається числом Рейнольдса Re (1.87). Якщо число Рейнольдса менше деякого критичного значення 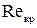, рух рідини буде ламінарним, в протилежному випадку – турбулентним.

Якщо тіло, яке рухається в рідині, має форму кулі діаметром d, то

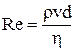, (1)

де ρ – густина рідини (в нашому випадку 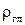); η – коефіцієнт внутрішнього тертя рідини; v – швидкість руху кульки.

При цьому критичне значення числа 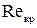= 0,5.

Виразимо швидкість кульки, розглянувши сили, які діють на неї у процесі руху. На кульку діють три сили:

1) сила тяжіння кульки (1.44)

,

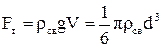де 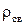– густина свинцю, V – об’єм кульки;

2) виштовхуюча сила 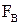, яка визначається за законом Архімеда (1.82),

,

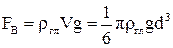де 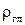– густина гліцерину;

3) сила внутрішнього тертя 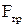, яка визначається формулою Стокса (1.86),

.

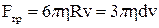При установленому русі кульки в рідині (v=const) сила тяжіння урівноважується сумою виштовхуючої сили та сили внутрішнього тертя,

тобто = + ,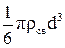

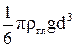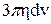звідки 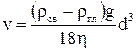. (2)

Сумісний розв’язок рівнянь (1) і (2) відносно d, дає

.

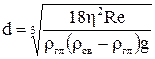Максимальне значення діаметра кульки відповідає критичному значенню числа Рейнольда. Тому

.

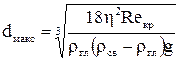Перевіряємо розмірність

.

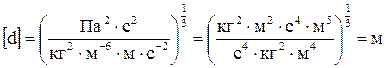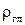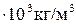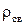Знаходимо з таблиці значення =1,26 ; =11,3 .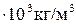

Підставляємо значення величин в отриману формулу

.

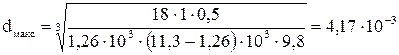Відповідь: 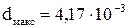м.

Дата добавления: 2015-01-03