Елементи динаміки

1. Динаміка матеріальної точки й тіла при поступальному русі.

Другий закон Ньютона

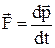, (1.40)

де 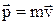– імпульс тіла.

Якщо сила, що діє на тіло, постійна за величиною та напрямком, то зміна імпульсу тіла за проміжок часу 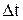дорівнює імпульсу сили, тобто добутку сили на час її дії:

. (1.41)

Якщо m=const, другий закон Ньютона може бути виражений формулою

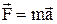, (1.42)

де 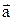– прискорення.

ІІІ закон Ньютона 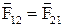(1.43)

де і 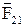- сили взаємодії двох матеріальних точок або сил.

Сили, що розглядають у механіці:

а) сила тяжіння

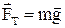, (1.44)

де 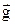- прискорення вільного падіння;

б) сила гравітаційної взаємодії

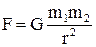, (1.45)

де G – гравітаційна стала, 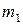і 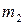–маси тіл (тіла вважають матеріальними точками), r – відстань між тілами;

в) сила тертя

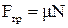, (1.46)

де μ – коефіцієнт тертя, N – сила реакції опору, яка за величиною дорівнює силі нормального тиску ;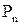

г) сила пружності 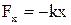, (1.47)

де k – коефіцієнт пружності (у випадку пружини – її жорсткість), 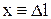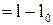– абсолютна деформація розтягу; 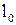і 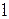– довжина до і після деформації відповідно.

Закон Гуку (1.47) для деформації розтягу або стиску може бути записаний у вигляді

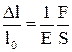, (1.48)

де 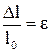- відносна деформація; Е – модуль Юнга; F – сила, що розтягує або стискує тіло; S – площа перерізу тіла; 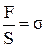– механічне напруження.

Інакше 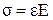. (1.49)

Порівняння формул (1.47) та (1.48) дає для коефіцієнта жорсткості вираз:

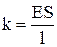. (1.50)

2. Динаміка руху твердого тіла, яке обертається навколо нерухомої осі.

Момент інерції І матеріальної точки відносно довільної осі

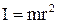(1.51)

де m – маса точки; r – відстань від точки до осі.

Момент інерції:

а) тонкостінного циліндра (тонкого кільця) відносно осі, що збігається з віссю циліндра (кільця),

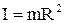, (1.52)

де R – радіус циліндра (кільця), m – його маса;

б) суцільного однорідного циліндра (диска) радіуса R відносно його осі

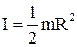; (1.53)

в) однорідного стержня масою m, що має довжину l, відносно осі, яка проходить через центр мас перпендикулярно до осі стержня,

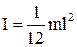; (1.54)

г) однорідної кулі масою m і радіуса R відносно осі, яка проходить через центр кулі, тобто збігається з діаметром кулі

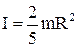. (1.55)

Теорема Гюйгенса – Штейнера дозволяє виразити момент інерції тіла І відносно довільної осі

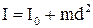, (1.56)

де – момент інерції тіла відносно осі, що проходить через центр мас паралельно даній осі, d – відстань між осями.

Момент сили відносно деякої осі Оz

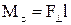, (1.57)

де 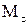– проекція сили на площину, яка э перпендикулярною до осі Оz, l – плече сили.

Момент імпульсу твердого тіла відносно осі обертання Оz

, (1.58)

де 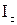– момент інерції тіла відносно осі Оz, 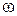– кутова швидкість.

Рівняння динаміки обертального руху твердого тіла навколо нерухомої осі Оz

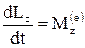, (1.59)

де 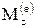– алгебраїчна сума моментів усіх зовнішніх сил, що діють на тіло, відносно осі Oz.

Якщо момент інерції залишається постійним у процесі руху, рівняння (1.59) набуває вигляду

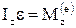, (1.60)

де ε – кутове прискорення.

3. Рівняння руху частинки відносно неінерціальної системи відліку К′

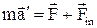, (1.61)

де – прискорення частинки в системі відліку К′, – сила, що діє на частинку з боку інших тіл, 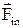– сила інерції.

При поступальному русі неінерціальної системи відліку К′ відносно інерціальної системи К з прискоренням 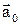сила інерції

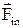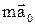= – . (1.62)

Рівняння руху частинки в неінераціальній системі відліку, яка обертається зі сталою кутовою швидкістю 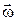відносно нерухомої осі

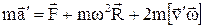, (1.63)

Тут відцентрова сила інерції

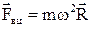, де ( 1.64)

– вектор, що лежить у площині обертання і проведений від осі обертання до частинки.

Дата добавления: 2015-01-03