Сила Коріоліса

, де (1.65)

- швидкість, з якою частинка рухається відносно неінерціальної системи відліку К′.

2. Закони збереження в механіці.

Зміна імпульсу незамкненоїсистеми

, (1.66)

де і – імпульси системи в моменти часу і 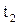, – результуюча всіх зовнішніх сил.

Якщо =0 (система замкнена), виконується закон збереження імпульсу

, (1.67)

де n – кількість тіл системи.

Зміна моменту імпульсу твердого тіла при обертанні відносно нерухомої осі згідно (1.59)

. (1.68)

Якщо 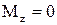(система замкнена), виконується закон збереження моменту імпульсу відносно осі Oz

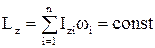. (1.69)

Робота змінної сили на шляху s

,

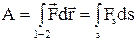де –модуль елементарного переміщення , – проекція сили на напрям елементарного переміщення, α – кут між векторами сили і переміщення.

У випадку постійної сили, що діє під кутом α до переміщення,

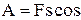α. (1.70)

Робота зовнішньої сили при обертанні твердого тіла

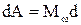φ, (1.71)

де 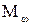– проекція моменту сили на напрям вектора кутової швидкості 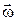, dφ – кут, на який повертається тіло.

Миттєва потужність

α, (1.72)

де α – кут між векторами сили і швидкості.

Кінетична енергія тіла маси m, що рухається із швидкістю ,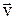

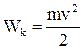. (1.73)

Кінетична енергія тіла, що обертається навколо нерухомої осі,

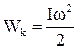. (1.74)

Кінетична енергія тіла у випадку плоского руху

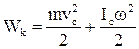, (1.75)

де 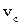– швидкість центра мас, – момент інерції тіла відносно осі, що проходить через центр мас паралельно миттєвій осі обертання.

Приріст кінетичної енергії частинки (теорема про кінетичну енергію)

, (1.76)

де А – робота результуючої всіх сил, що діють на частинку.

Потенціальна енергія:

а) тіла в однорідному полі сили тяжіння Землі (поблизу поверхні Землі)

, (1.77)

де g – прискорення вільного падіння, h– відстань між тілом і поверхнею Землі;

б) гравітаційної взаємодії двох тіл

, (1.78)

Знак „–” відповідає тому, що потенціальна енергія двох взаємодіючих тіл дорівнює нулю при 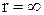і зменшується при їх наближенні;

в) потенціальна енергія при пружній деформації тіла (пружини)

. (1.79)

Зв’язок між роботою консервативних сил та потенціальною енергією системи (тіла) у початковому та кінцевому станах

. (1.80)

Закон збереження механічної енергії для консервативної системи

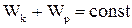. (1.81)

4. Елементи механіки рідини та газів.

Сила, що діє на занурене в рідину або газ тіло (закон Архімеда)

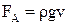, (1.82)

де ρ – густина рідини або газу, g – прискорення вільного падіння, V – об’єм рідини або газу, що витиснуло тіло.

Рівняння нерозривності струменю

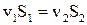, (1.83)

де 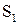, – площі перерізу струменю, , 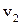– відповідні швидкості течії.

Рівняння Бернуллі (для стаціонарного потоку ідеальної рідини)

, (1.84)

де ρ – густина рідини, v – швидкість течії в деякому перерізі струмини, h – висота даного перерізу над рівнем відліку, р – тиск рідини в перерізі.

Швидкість витікання ідеальної рідини крізь малий отвір у широкій посудині (формула Торрічеллі)

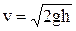(1.85)

де h – висота стовпа рідини над отвором.

Сила опору при русі кулі у в’язкому середовищі або при обтіканні нерухомої кулі (формула Стокса)

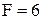πη 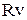, (1.86)

де η – динамічна в’язкість рідини (газу), R – радіус кулі, v – швидкість.

Формула Стокса є справедливою тільки при ламінарній течії.

При ламінарній течії об’єм рідини, яка проходить крізь трубку завдовжки 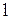і радіуса R за час t, визначається за формулою Пуазейля

,
де – різниця тисків на кінцях трубки.

Характер течії рідини (газу) визначається числом Рейнольдса

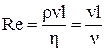, (1.87)

де l – характерний лінійний розмір тіла, v – швидкість течії, η – динамічна в’язкість, – кінематична в’язкість. Критичне значення числа Рейнольдса, яке визначає перехід від ламінарної течії до турбулентної, є різним для тіл різної форми.

Дата добавления: 2015-01-03