Елементи кінематики

Основні формули

ФІЗИЧНІ ОСНОВИ КЛАСИЧНОЇ МЕХАНІКИ

1. Положення матеріальної точки (центра мас твердого тіла) у просторі задається радіусом-вектором

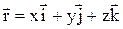, (1.1)

де 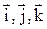- одиничні вектори напрямів (орти); x, y, z – координати точки.

Кінематичне рівняння руху матеріальної точки надає залежність її координат від часу

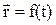. (1.2)

Миттєва швидкість частинки

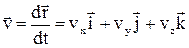, (1.3)

де 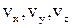- проекції швидкості на осі координат; x, y, z – координати точки.

Середня швидкість за час ∆t

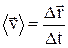, (1.4)

де 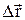- переміщення матеріальної точки за час ∆t.

Модуль вектора швидкості

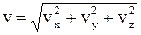. (1.5)

Напрямок миттєвої швидкості у кожній точці траєкторії співпадає з напрямком дотичної до траєкторії у тій самій точці.

Прискорення

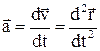. (1.6)

Для визначення миттєвого прискорення 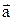при криволінійному русі його розкладають на дві складові: тангенціальне прискорення 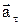та нормальне (доцентрове) прискорення 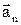(рис. 1.1).

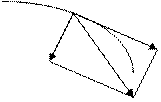
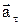
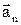
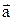
Рис. 1.1.

Тангенціальне прискорення характеризує зміну швидкості за величиною, спрямовано по дотичній і дорівнює

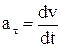. (1.7)

Нормальне прискорення характеризує зміну швидкості за напрямком, спрямовано до центру кривизни траєкторії і знаходиться за формулою

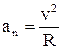, (1.8)

де R – радіус кривизни траєкторії.

Повне прискорення

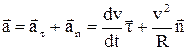(1.9)

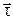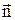, - орти (одиничні вектори) дотичної та нормалі до траєкторії.

Величина прискорення обчислюється за формулою

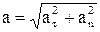(1.10)

Шлях, який пройшла точка,

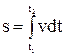. (1.11)

2. При прямолінійному русі вздовж осі Ох положення точки визначається її координатою x.

Значення середньої швидкості у цьому випадку

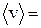
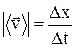, (1.12)

де 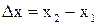- зміна координати за проміжок часу .

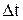На практиці розглядають також скалярну середню швидкість (швидкість на шляху s)

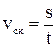. (1.13)

На відміну від різниці координат 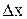шлях не може зменшуватися й приймати негативні значення.

Отже, якщо точка рухається вздовж прямої в одному напрямку, її шлях 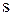співпадає з різницею координат .

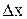У випадку, коли в деякий момент часу напрямок руху змінюється на протилежний, координата з даного моменту часу зменшується, а шлях продовжує зростати. Тоді

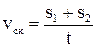, (1.14)

де 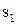та 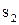- шляху, що пройдені до та після повороту.

Миттєва швидкість

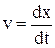. (1.15)

Середнє прискорення

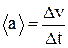. (1.16)

Миттєве прискорення співпадає з тангенціальним ; .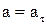

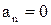. (1.17)

Рівняння рівнозмінного прямолінійного руху вздовж осі Ох (тобто, при )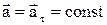

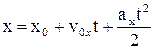, (1.18)

де 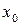- координата точки в момент часу t=0; 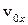та 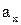– проекції швидкості та прискорення точки на координатну ось.

Проекція 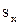переміщення на координатну ось

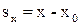
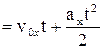. (1.19)

Швидкість рівнозмінного руху

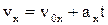. (1.20)

З рівнянь (1.19) і (1.20) випливає корисна формула:

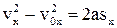. (1.21)

Рівняння рівномірного руху ()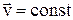

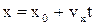, (1.22)

або

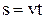(1.23)

1. При обертанні тіла навколо нерухомої осі будь-яка точка описує коло, площина якого перпендикулярна до осі обертання, і центрякого лежить на вісі. Для опису руху зручно користуватися кутовими змінними.

Кінематичне рівняння обертального руху

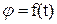, (1.24)

де φ – кут повороту вектора , проведеного із центра кола, вздовж якого рухається будь-яка точка тіла, до цієї точки.

Середня кутова швидкість

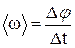. (1.25)

Кутова швидкість (за величиною)

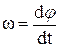. (1.26)

Середнє кутове прискорення

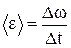, (1.27)

де 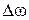- зміна кутової швидкості за час .

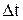Кутове прискорення (за величиною)

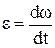. (1.28)

Рівняння рівнозмінного обертання ()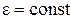

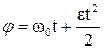. (1.29)

Кутова швидкість рівноприскореного обертання

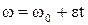, (1.30)

де ε>0 при прискореному русі і ε<0 при уповільненому русі.

Після виключення з рівнянь (1.29) і (1.30) часу t отримуємо

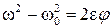. (1.31)

Рівняння рівномірного обертання ()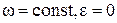

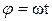. (1.32)

Зверніть увагу на те, що формули (1.25) – (1.32) аналогічні формулам (1.15) – (1.23) для прямолінійного руху точки.

Частота обертання (кількість оборотів за одиницю часу)

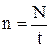, (1.33)

або

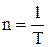, (1.34)

де N – кількість оборотів за час t; T – період обертання (час, за який здійснюється один оборот).

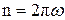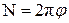; . (1. 35)

Зв’язок між величинами лінійних і кутових змінних надається формулами:

довжина дуги, що пройдена точкою,

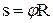, (1.36)

де 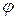- кут обертання тіла, R – радіус обертання точки;

лінійна швидкість точки

v = 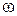R; (1.37)

тангенціальне прискорення точки

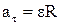; (1.38)

нормальне прискорення точки

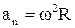. (1.39)

Дата добавления: 2015-01-03