Основні формули. Кількість речовини тіла (системи)

МОЛЕКУЛЯРНА ФІЗИКА ТА ТЕРМОДИНАМІКА.

Кількість речовини тіла (системи)

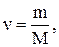(2.1)

де m – маса тіла m – молярна маса.

Кількість структурних елементів (атомів, молекул і т.п.) у тілі (системі)

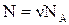(2.2)

де 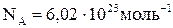– постійна Авогадро.

Рівняння стану ідеального газу (рівняння Менделєєва – Клапейрона)

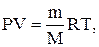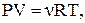або (2.3)

де P – тиск газу, V – його об’єм; m – маса газу; M– молярна маса газу; R = 8,31 Дж / (моль × K) – універсальна газова стала; T – термодинамічна температура.

T = 273 + t (2.4)

де t – температура за шкалою Цельсія.

Окремі випадки рівняння стану (ізопроцеси):

а) закон Бойля – Маріотта (ізотермічний процес, T = const, m = const)

PV = const, або 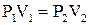(2.5)

б) закон Гей – Люссака (ізобаричний процес, P = const)

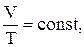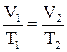або (2.6)

в) закон Шарля (ізохоричний процес, V = const)

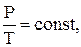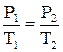або (2.7)

Тиск у суміші газів визначається за законом Дальтона.

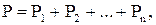(2.8)

де 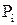– парціальний тиск окремих компонентів, n – кількість компонентів.

Концентрація молекул речовини у будь-якому стані

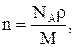або (2.9)

де N – кількість молекул, які містяться у даній системі; V – об’єм тіла або системи; r - густина речовини; M– молярна маса речовини.

Основне рівняння кінетичної теорії газів

(2.10)

де n – концентрація молекул, – середня кінетична енергія молекули.

Для одноатомної молекули

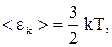(2.11)

де – постійна Больцмана; T – термодинамічна температура.

Для багатоатомної молекули

(2.12)

де і – кількість ступенів свободи молекули.

Зв’язок тиску газу з концентрацією і температурою

p = nkT (2.13)

Швидкість руху молекул:

– середня квадратична, (2.14)

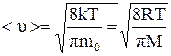– середня арифметична, (2.15)

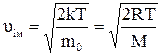– найбільш ймовірна, (2.16)

де 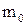– маса однієї молекули.

Середня довжина вільного пробігу молекули

(2.17)

де s – ефективний діаметр молекули; n – концентрація молекул.

Середнє число зіткнень кожної молекули з іншими в одиницю часу

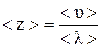(2.18)

Молярні теплоємності газу при постійному об’ємі () і при постійному тиску ():

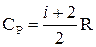(2.19)

Згідно з рівнянням Роберта Майєра

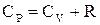(2.20)

Зв’язок між молярною (С) і питомою (с) теплоємностями

(2.21)

Перше начало термодинаміки

Q = DU + A (2.22)

де Q – теплота яку надано системі; DU – зміна внутрішньої енергії системи; A – робота системи проти зовнішніх сил.

Внутрішня енергія ідеального газу

(2.23)

Робота розширення газу у загальному випадку

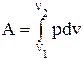(2.24)

Окремі випадки:

а) ізобаричний процес: 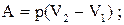(2.25)

б) ізотермічний процес: 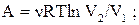(2.26)

в) адіабатичний процес (який відбувається без теплообміну з оточуючим середовищем, Q = 0):

(2.27)

де – молярна теплоємність при постійному об’ємі;

– коефіцієнт Пуассона.

При адіабатичному процесі параметри стану зв’язані рівняннями:

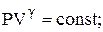
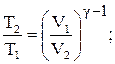
(2.28)

Термодинамічний коефіцієнт корисної дії (к.к.д.) теплової машини

або (2.29)

де – теплота, яку отримало робоче тіло машини за один цикл;

– теплота, яку робоче тіло віддало за цикл;

– робота, яку виконало робоче тіло за цикл.

Для циклу Карно

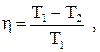(2.30)

де 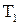– температура нагрівача, 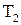– температура охолоджувача.

Зміна ентропії для елементарного процесу

(2.31)

де – кількість отриманої системою тепла; T – температура, при якій відбувається теплопередача.

При наявності у просторі градієнтів температури, густини речовини, або якщо межують шари рідини або газу, що рухаються з різними швидкостями, виникають процеси по вирівнюванню цих неоднорідностей (явища переносу).

У одномірному випадку вони відбуваються за законами

а) для теплопровідності: 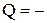c (2.32)

де Q – кількість теплоти, перенесена за час Dt крізь площадку DS;

DT/DX – градієнт температури у напрямку, перпендикулярному до DS;

c – коефіцієнт теплопровідності.

б)для дифузії: (2.33)

M – маса, перенесена за час Dt крізь площадку DS,

– градієнт густини у напрямку, перпендикулярному до площадки; D – коефіцієнт дифузії.

в) для внутрішнього тертя (в’язкості):

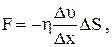(2.34)

де F – сила внутрішнього тертя; Du/Dx – градієнт швидкості течії газу у напряму, перпендикулярному до DS; h – коефіцієнт внутрішнього тертя (динамічна в’язкість).

Для коефіцієнтів справедливі співвідношення

c (2.35)

Окремі випадки розподілу Гіббса:

а) розподіл молекул по швидкостям (закон Максвелла)

(2.36)

де DN – кількість молекул, відносні швидкості яких лежать в інтервалі від u до u + Du; – відносна швидкість, u – швидкість молекули і

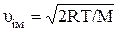– найбільш імовірна швидкість молекул;

N – загальне число молекул;

При розв’язуванні задач на розподіл молекул по швидкостям зручно використовувати таблицю (1)

Таблиця 2.1

U		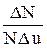U		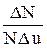U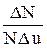
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8	0,02 0,09 0,18 0,31 0,44 0,57 0,68 0,76	0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7	0,81 0,83 0,82 0,78 0,71 0,63 0,54 0,46 0,36	1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5	0,29 0,22 0,16 0,12 0,09 0,06 0,04 0,03

б) барометрична формула (у припущенні, що температура в усіх точках однакова) дає залежність тиску газу від висоти h в полі сили тяжіння

(2.37)

де – тиск на висоті h = 0; g – прискорення сили тяжіння.

Рівняння стану реального газу (рівняння Ван-дер-Ваальса) для одного моля

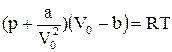(2.38)

де 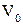– об’єм моля; a і b – постійні, які залежать від природи газу.

Рівняння для будь-якої кількості газу

(2.39)

Постійні a і b зв’язані з критичними параметрами співвідношеннями

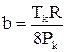(2.40)

Дата добавления: 2015-01-03