Типовые задачи. По данным задачи требуется рассчитать средние значения по каждому признаку:

Задача 1.

По данным задачи требуется рассчитать средние значения по каждому признаку:

К – количество студентов в институте;

С – процент студентов в институте, не получающих стипендию;

Р – средний размер стипендии одного студента-стипендиата.

Институт	К	С	Р

Решение

1) Среднее количество студентов в институте определяется по средней арифметической простой:

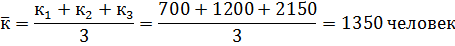
2) Средний процент студентов, не получающих стипендию, определяется с помощью средней арифметической взвешенной, причем в качестве весов используется численность студентов в институте.

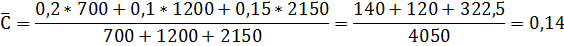
Средний процент студентов, не получающих стипендию равен 14%.

3) Средний размер стипендии в среднем на одного студента-стипендиата вычисляется по средней арифметической взвешенной, причем в качестве весов используется количество студентов, получающих стипендию в каждом институте.

В первом институте количество студентов, получающих стипендию равно 700 – 0,2*700 = 700-140 = 560 чел., где 140 – число студентов, не получающих стипендию в первом институте.

Во втором институте количество студентов, получающих стипендию равно 1200 – 0,10*1200 = 1200 – 120 = 1080 чел., где 120 – число студентов, не получающих стипендию во втором институте.

Во третьем институте количество студентов, получающих стипендию равно 2150 – 0,15*2150 = 2150 – 322,5 = 1827,5 чел. где 322,5 – число студентов, не получающих стипендию в третьем институте.

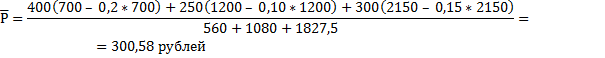
Таким образом, средний размер стипендии по трём институтам составляет 300,58 руб.

Рассмотрим усложнённый вариант исходных данных и особенности выбора формулы для вычисления среднего значения признака. Для этого необходимо составить исходное соотношение средней в виде отношения двух признаков, отражающего сущность осредняемого признака, его логическое содержание. Например, средняя заработная плата определяется как отношение фонда оплаты труда к численности работников:

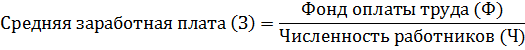
Или средние трудозатраты на выпуск единицы изделия можно определить как отношение суммарных трудозатрат на выпуск всей партии изделий на количество выпущенных изделий.

Суммарные трудозатраты на выпуск

Средние трудозатраты ­­­­­­­­­­­­­­­­­­всех изделий (∑ Т)

на единицу изделия (Т) =

Количество изделий (К)

Если при вычислении среднего значения признака в качестве весов-соизмерителей берётся числитель исходного соотношения, то используется формула средней гармонической взвешенной.

Используя в качестве весов-соизмерителей знаменатель соответствующего отношения при вычислении среднего значения признака выбирается формула средней арифметической взвешенной.

Задача 2.

По данным задачи требуется рассчитать средние значения по каждому признаку:

С – число студентов на факультете;

Г – среднее число студентов в группе;

Д – доля студентов-иностранцев на факультете, %;

Б – средний балл успеваемости одного студента в сессию.

Факультеты	С	Г	Д	Б
I			2,0	4,4
II			8,3	4,0
III		23,5	10,1	4,6
IV			7,0	4,2

Решение

1) Среднее количество студентов на факультете определяется с помощью средней арифметической простой:

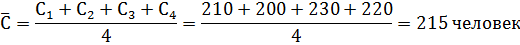
2) Для того чтобы правильно выбрать формулу для вычисления среднего числа студентов в группе, необходимо составить исходное соотношение средней, отражающее сущность осредняемого признака. Исходное соотношение для нахождения среднего числа студентов в группе будет выглядеть следующим образом:

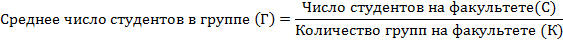
Зная количество студентов на факультете, т.е. числитель данного отношения, при вычислении среднего числа студентов в группе по четырём факультетам (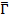) будем использовать среднюю гармоническую взвешенную.

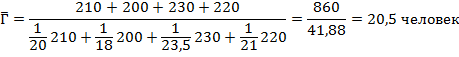
Таким образом, в каждой группе в среднем учатся 20,5 человека.

Однако можно определить и знаменатель исходного соотношения - количество групп на каждом факультете. Оно вычисляется путём отношения числа студентов на факультете к среднему числу студентов в группе.

Таким образом, определим количество групп на каждом факультете:

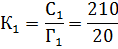
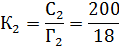
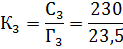
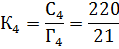
Определив знаменатель исходного соотношения, вычислим среднее число студентов в группе по четырём факультетам по средней арифметической взвешенной, используя в качестве весов-соизмерителей количество групп на факультете.

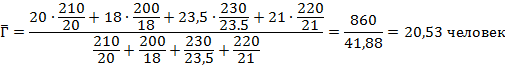
Результаты вычисления среднего числа студентов в группе по средней арифметической взвешенной и средней гармонической взвешенной полностью совпадают.

3) Средняя доля студентов-иностранцев на факультете (%) определяется с помощью средней арифметической взвешенной – в качестве весов используется число студентов на факультете:

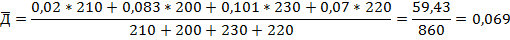
то есть средний процент студентов-иностранцев по всем факультетам равен 6,9%.

4) Средний балл успеваемости одного студента в сессию по всем факультетам можно представить в виде исходного соотношения:

Общий (суммарный) балл, полученный

Средний балл всеми студентами в сессию (ОБ)

успеваемости =

одного студента (Б) Число студентов (С)

По условию задачи имеется знаменатель данного отношения (C), соответственно при вычислении среднего значения признака выбирается средняя арифметическая взвешенная и в качестве весов используется число студентов (С).

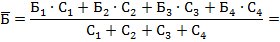
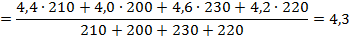
Таким образом, средний балл, получаемый студентами в сессию по всем факультетам равен 4,3.

При этом среднее значение признака (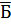) можно вычислить по средней гармонической взвешенной, используя в качестве весов числитель исходного соотношения.

Числитель исходного соотношения – общий (суммарный) балл (ОБ), полученный всеми студентами в сессию может быть вычислен путём умножения среднего балла одного студента в сессию (Б) на число студентов на факультете (C). Вычислим суммарные баллы, полученные всеми студентами в сессию для каждого факультета.

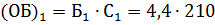
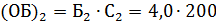
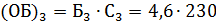
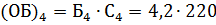
Отсюда средний балл вычислим как:

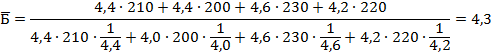
Результаты вычисления среднего балла (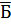) по средней арифметической взвешенной и средней гармонической взвешенной полностью совпадают.

Задача 3.

Имеются данные о перевозке грузов железнодорожным транспортом (млн. т.) в Российской Федерации:

Годы
Перевезено грузов, млн. т.

Определить среднегодовой темп (коэффициент) роста объёма перевозок железнодорожным транспортом.

Решение

Определим цепные коэффициенты роста объёма грузовых перевозок, которые показывают, во сколько раз объём перевозок текущего года изменился по отношению к объёму перевозок предыдущего года.

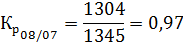
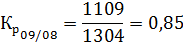
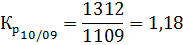
Так как коэффициенты роста связаны между собой знаком произведения, средний коэффициент роста вычисляется по средней геометрической:

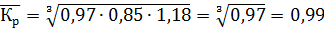
Таким образом, среднегодовой темп роста объёма перевозок грузов железнодорожным транспортом в Российской Федерации в период с 2007 по 2010 годы составил 99%.

Задача 4.

Подача жидкого топлива для технологического процесса осуществляется в цехе тремя трубопроводами с диаметрами 2 см, 5 см и 6 см. При капитальном ремонте здания цеха эти трубопроводы будут заменены на 3 новых трубопровода одинакового диаметра при сохранении их общей пропускной способности. Определить средний диаметр трубы (диаметр новой трубы).

Решение

Пропускная способность трубы зависит от площади сечения трубы (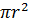), а соответственно определяющим показателем пропускной способности трубы является её радиус.

Радиус первой трубы: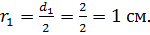

Площадь сечения 1-ой трубы определяется как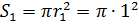

Радиус второй трубы: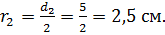

Площадь сечения 2-ой трубы определяется как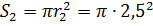

Радиус третьей трубы: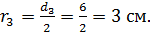

Площадь сечения 3-ой трубы определяется как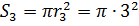

Сохранение общей пропускной способности новых труб достигается сохранением их общей площади сечения, то есть

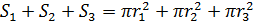
Таким образом, на выходе необходимо сохранить сумму квадратов радиусов, а значит при расчёте среднего значения признака применим среднюю квадратическую.

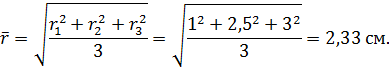
Итак, средний диаметр трубы равен:

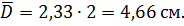
Дата добавления: 2014-12-24