Типовые задачи

Задача 1.

Имеются следующие данные о возрастном составе рабочих цеха (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29.

Для анализа распределения рабочих цеха по возрасту требуется:

1) Построить интервальный ряд распределения.

2) Дать графическое изображение ряда.

3) Вычислить показатели центра распределения.

4) Сформулировать выводы.

Решение

1) Величину интервала определим с помощью формулы:

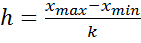, где k – количество групп, определяемое с помощью формулы Стержесса: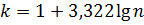

n – общее число единиц совокупности; n =30, следовательно k» 6.

x_max = 38 лет, x_min = 18 лет, отсюда ширина интервала

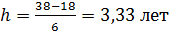» 3,5 лет

Построенный интервальный ряд распределения имеет вид:

Группы рабочих по возрасту (лет), xi	Число рабочих, fi	Накопленная частота, Si
18 – 21,5
21,5 – 25
25 – 28,5
28,5 – 32
32 – 35,5
35,5 – 39

2) Графически интервальный вариационный ряд может быть представлен в виде гистограммы распределения (рис.1):

Рисунок 1 – Гистограмма и полигон распределения

На отрезках (интервалах) по оси x строятся прямоугольники, высота которых соответствует частоте. На основе построенной гистограммы графически можно определить значение моды. Для этого правую вершину модального прямоугольника соединяют прямой с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяют с левым верхним углом последующего прямоугольника. Из точки пересечения этих прямых опускают перпендикуляр на ось x. Координата пересечения перпендикуляра и оси x является модой распределения.

Для преобразования гистограммы в полигон распределения середины верхних сторон прямоугольников соединяют отрезками прямой. Для замыкания полигона из крайних точек (слева и справа на ломаной линии) опускают перпендикуляры на ось x.

На рис. 2 представлена кумулята распределения или кумулятивная кривая:

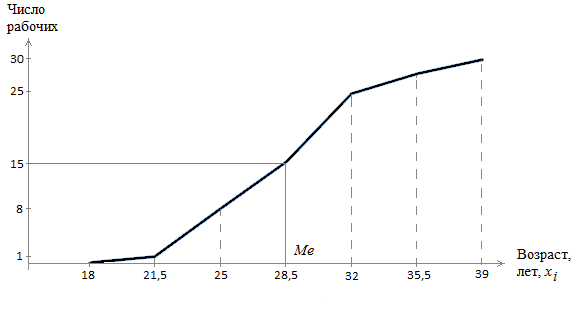
Рисунок 2 – Кумулята распределения

Кумулята может быть использована для графического определения медианы. Для этого половину объёма совокупности отмечают на оси y. Через полученную точку проводят прямую, параллельную оси x, до пересечения её с кумулятой. Из точки пересечения опускают перпендикуляр до оси x. Координата точки пересечения перпендикуляра с осью x является медианой.

3) Для анализа вариационных рядов используются показатели центра распределения: средняя арифметическая, мода и медиана.

Для расчёта среднего значения признака в интервальном вариационном ряду используется средняя арифметическая взвешенная. При этом в качестве индивидуальных значений признака берутся середины соответствующих интервалов ():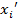

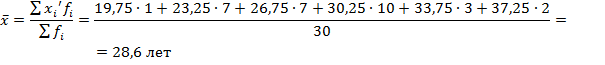
Таким образом, средний возраст рабочих цеха составляет 28,6 лет.

При определении моды сначала находят интервал, содержащий моду. Модальным интервалом в данном распределении является 28,5-32, так как наибольшее число рабочих (f =10) находится в этом интервале. Значение моды определяется по формуле:

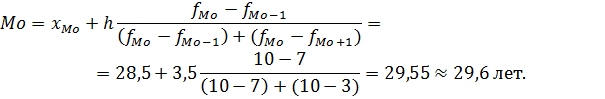
Таким образом, наибольшее количество рабочих цеха находятся в возрасте 29,6 лет.

Медианным является интервал 25-28,5. Медианному интервалу соответствует половина накопленных частот совокупности (S_i). В данном случае это 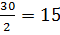рабочих. Значение медианы определяется по формуле:

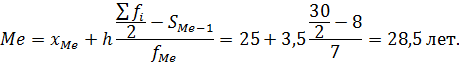
Половина рабочих цеха находится в возрасте от 18 до 28,5 лет, а вторая половина рабочих в возрасте от 28,5 до 38 лет.

Задача 2.

По приведённым ниже данным о квалификации рабочих цеха требуется:

1) построить дискретный ряд распределения;

2) дать графическое изображение ряда;

3) вычислить показатели центра распределения;

4) вычислить показатели вариации.

Тарифные разряды 24 рабочих цеха: 4; 3; 6; 4; 4; 2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3.

Решение

1) Построим дискретный вариационный ряд

Тарифный разряд,	Число рабочих,	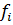Накопленная частота, S i
Итого		-

2) Представим графическое изображение построенного дискретного вариационного ряда в виде полигона распределения (рис. 3)

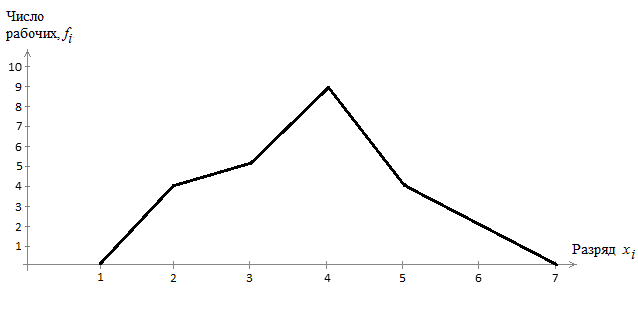
Рисунок 3 – Полигон распределения рабочих по тарифному разряду

3) Вычислим показатели центра распределения. Среднее значение признака вычисляется по средней арифметической взвешенной:

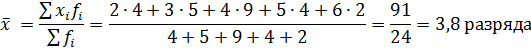
Значение моды определяется так: Mo =4-му разряду, так как данному значению признака соответствует наибольшая частота (f = 9). Таким образом, наибольшее число рабочих имеют 4-й разряд.

Медиана в дискретном вариационном ряду с чётным количеством значений определяется как средняя из двух смежных серединных значений. В данном дискретном вариационном ряду n=24, соответственно серединными значениями признака являются значения под номерами 12 и 13. Номер 12 и 13 соответствуют 4-му разряду. Соответственно

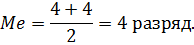
Таким образом, половина рабочих имеют тарифный разряд меньше 4-го, а вторая половина рабочих имеют разряд больше 4-го.

4) К показателям вариации относятся: размах, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации.

Для вычисления показателей вариации воспользуемся вспомогательной таблицей.

Тарифный разряд,	Число рабочих,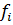
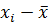
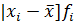
		-1,8	7,2	12,96
		-0,8	4,0	3,20
		+0,2	1,8	0,36
		+1,2	4,8	5,76
		+2,2	4,4	9,68
Итого			22,2	31,96

Среднее линейное отклонение вычисляется следующим образом:

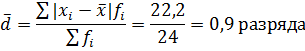
Вычислим среднее квадратическое отклонение:

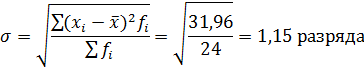
Таким образом, индивидуальные значения признака (тарифные разряды) отличаются в среднем от средней арифметической на 1,15 разряда.

Вычислим относительную меру вариации в виде коэффициента вариации:

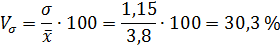
Значение коэффициента вариации свидетельствует о том, что совокупность достаточно однородна.

Вычислим показатель асимметрии (показатель Пирсона):

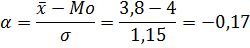
Следовательно, асимметрия левосторонняя, слабая.

Дата добавления: 2014-12-24