Мощность в цепи синусоидального переменного тока

Энергетические процессы в цепях синусоидального переменного тока представляют более сложную картину в сравнении с цепями постоянного тока, т. к. в них участвуют накопители энергии – индуктивности и емкости. Одной из характеристик энергетического процесса является мощность.

Наиболее простым является понятие мгновенной мощности. Для резистора, на котором напряжение и ток совпадают по фазе, мощность определяется следующим выражением:

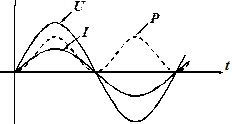Рис. 2.3.1

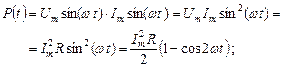(2.3.1)

т. е. мгновенная мощность имеет в себе постоянную состав­ля­ющую и колеба­тель­ную с частотой 2 w, как изобра­жено на рис. 2.3.1. Мгновенная мощ­ность не всегда удобна для практической деятельности, чаще нас интересует некая средняя за период колебания мощность, выделяемая на резисторе, называемая актив­ной мощностью:

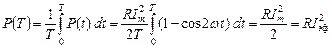. (2.3.2)

Здесь I _эф – действующее (эффективное) значение тока, равное среднеквадратичному значению тока за период:

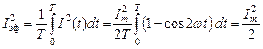. (2.3.3)

Действующее значение переменного тока численно равно такому значению постоянного тока, который выделит на резисторе ту же энергию за определенный период времени, что и переменный. После введения действующих значений переменного тока и напряжения выражения мощности получаются такими же, что и для цепей постоянного тока:

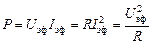. (2.3.4)

На индуктивном сопротивлении между током и напряжением имеется фазовый сдвиг 90°

.

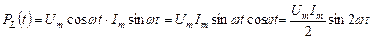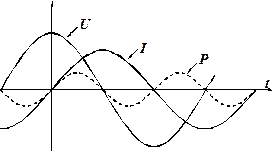Рис. 2.3.2

На рис. 2.3.2 показан временной график изменения мощности на индук­тивном сопротив­ле­нии, где видно, что имеет место коле­бание мощнос­ти с удвоен­ной частотой, посто­ян­ная сос­тав­ля­ющая от­сутст­вует.

Физически это можно интерпретировать так, что в течение 1/4 периода колеба­ния тока энергия погло­ща­ет­ся индуктив­ностью, мощ­ность услов­но считают поло­жи­тель­ной. В течение следу­ю­щей четверти периода мощность отрицательна, т. е. энергия, накопленная в индуктивности, возвращается во внешнюю цепь обратно, на этот отрезок времени индуктивность становится источником энергии.

В среднем за период мощность оказывается равной нулю – в стационарном режиме катушка индуктивности не потребляет энергию от источника.

Проинтегрировав мощность за время равное 1/4 периода, можно найти максимальную энергию, накапливаемую в индуктивности:

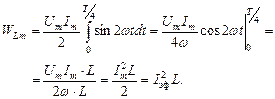(2.3.6)

На емкостном сопротивлении между током и напряжением, аналогично, имеет место фазовый сдвиг, но в противоположную сторону:

. (2.3.7)

Максимальная энергия, накапливаемая в емкости за четверть периода:

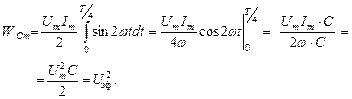(2.3.8)

в цепи, содержащей элементы R, L, C неизвестной величины, мгновенное значение мощности есть произведение мгновенных значений тока и напряжения:

.

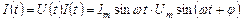Если это выражение проинтегрировать в пределах периода T и разделить на T, получим

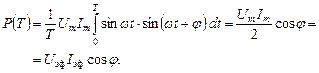(2.3.9)

Очевидно, что это есть мощность, рассеиваемая на резисторе, т. е. активная мощность, т. к. интегралы мощностей за период на индуктивности и емкости равны нулю.

Чтобы охарактеризовать присутствие энергии в индуктивности и емкости, вводится понятие реактивной мощности

Q (T)= U _эф I _эф sin j (2.3.10)

и полной мощности

S (T)= U _эф I _эф. (2.3.11)

Мощности P, Q и S связаны между собой следующим образом:

P = S× cos j, Q = S ×sin j, S ² = P ² + Q ². (2.3.12)

Показатель cos j, характеризующий присутствие в электрической цепи реактивной энергии, широко исполь­зуется в энергетике. Присутствие в цепях реактивных токов приводит к дополнительным потерям электри­ческой энергии в источниках и линиях электропередачи и уменьшению, т. о. коэффициента полезного действия цепи. Обычно причиной возник­новения реактивных токов являются индуктивные нагрузки (трансформаторы, электромоторы и т. д.). Способом увеличения показателя cos j в цепях является компенсация ин­дук­тивной составляющей нагрузки путем подклю­чения к ней емкости такой величины, чтобы выпол­нялось условие

.

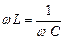В результате в подводящих проводах остается активная составляющая тока, а реактивная циркулирует в контуре, образованном нагрузкой и компенсирующим конденсатором, как показано на рис. 2.3.3.

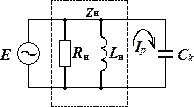
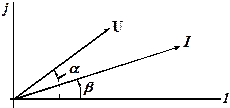
Рис. 2.3.3 Рис. 2.3.4a

Понятия активной, реактивной и полной мощности используются и в рамках символического метода. Однако необходимо иметь в виду, что простое перемножение комплексных величин 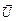и 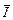, показанных на рис. 2.3.4а, не дает выражения мощности, необходимо вместо комплекса тока взять сопряженную ему величину

.

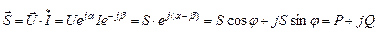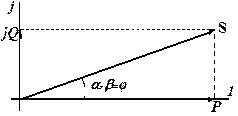Рис. 2.3.4b

Мощность 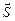называют ком­плексной мощностью. Модуль комплексной мощности равен полной мощности, а аргумент – углу сдвига фаз между напря­жением и током. Ее вещест­венная и мнимая составляющие представ­ля­ют соответственно актив­ную и реактивную мощ­ности, как пока­за­но на рис. 2.3.4b.

Комплексная мощность может быть выражена и через комплексное сопротивление:

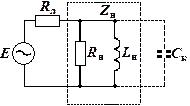Рис. 2.3.5

.

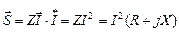Задача 2.3.1 (рис. 2.3.5). Источник э.д.с. и нагрузку Z _нсоединяет линия с сопро­тив­лением R _л = 40 Ом. Параметры нагрузки: P _н = 80 кВт, I _н = 10 А, cos j = 0,8. Частота э.д.с. 50 Гц. Найти э.д.с. источника E и КПД цепи. Далее, найти величину компенсирующей емкости, при которой cos j цепи равен 1, и снова найти КПД цепи.

Решение. Найдем КПД цепи:

.

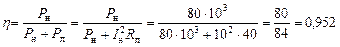Найдем полное сопротивление нагрузки

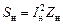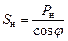, , откуда

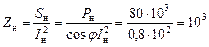Ом.

Представим нагрузку в виде последовательного соединения активного и реактивного сопротивлений: r _н и x _н. Тогда появляется возможность найти полное сопротивление всей цепи Z и величину э.д.с. источника E:

Z = R _л + r _н + j x _н = R _л + Z _нcos j + jZ _нsin j = (40 + 800 + j 600) Ом,

E = I _н Z = 10 (840 + j 600) = 10320 e ^{j 35,5°} В.

Найдем компенсирующую емкость С _к, для чего представим нагрузку в виде параллельного соединения активного и индуктивного сопротивлений R _н и X _н:

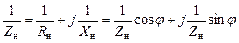, откуда

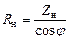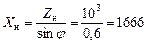и Ом.

Чтобы соблюсти условие X_C = X _н, потребуется емкость

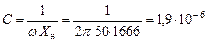Ф.

После компенсации сопротивление нагрузки станет активным и составит величину

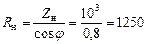Ом.

Полное сопротивление цепи составит величину

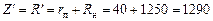Ом.

Коэффициент полезного действия

.

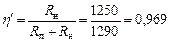Задача 2.3.2 (для самостоятельного решения). Определить, какой мощностью должен обладать трансформатор, если к нему подключить нагрузку, потребляющую мощность P = 10 Вт и имеющую cos j = 0,1.

Дата добавления: 2014-12-24