Переходные процессы в цепях синусоидального переменного тока

Формализация классического метода

Классический метод анализа переходного процесса

В классическом методе решения дифференциального уравнения коэффи­циенты p ₁, p ₂… p_N являются корнями т. н. характеристического уравнения. характеристическое уравнение можно получить, подставив результат решения однородной части дифференциального уравнения I (t) = I ₀(t) e^Pt в само уравне­ние (например, в уравнение 4.1.3 для цепи на рис. 4.1.1). Это называется алгебраизацией дифференциального уравнения.

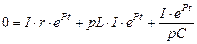, после сокращения

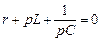. (4.2.1)

Решив уравнение (4.2.1), найдем его корни p ₁, p ₂. Теперь свободная составляющая решения (например, для тока) будет иметь вид

.

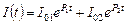Постоянные коэффициенты I ₀₁ и I ₀₂ находят из анализа начальных условий переходного процесса, т. е. мгновенных величин токов и напряжений в цепи в моменты времени t _0– и t ₀₊ (моменты, бесконечно близко прилегающие к моменту t ₀ начала переходного процесса, как показано, например, на рис. 4.2.2). Анализ начальных условий опирается на законы Кирхгофа и законы коммутации. Напомним законы коммутации.

1. Ток через индуктивность не может измениться мгновенно и в моменты t_0– и t₀₊ остается неизменным.

2. Напряжение на емкости не может измениться мгновенно и в моменты t_0– и t₀₊ остается неизменным.

Анализ начальных условий удобно проводить с помощью таблицы, куда заносятся значения токов и напряжений в цепи в моменты времени t _0– t ₀₊ и по окончании переходного процесса (обозначим t ® ¥).

Частное решение дифференциального уравнения отражает, по сути дела, новое стационарное состояние цепи по окончании переходного процесса (т. е. при t ® ¥).

Кратко сформулируем теперь алгоритм решения задачи о переходном процессе классическим методом:

1. Составляется дифференциальное уравнение (или система дифференциальных уравнений для многоконтурной цепи) по принципиальной схеме цепи. Уравнения составляются в форме уравнений Кирхгофа или используются методы контурных токов и узловых потенциалов.

2. Составляется характеристическое уравнение цепи (или система характеристических уравнений для многоконтурной цепи). Находятся корни характеристического уравнения.

3. Анализируется состояние цепи в моменты времени t _0– t ₀₊ и t ® ¥. Составляется таблица начальных условий цепи. На основании составленной таблицы находятся постоянные коэффициенты A ₁, A ₂… A_N для свободной части решения и A _пр для принужденной части решения (под символом A подразумеваются ток или напряжение).

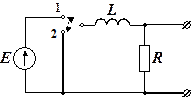Рис. 4.2.1

4. Рисуется график переходного процесса, на котором показываются как реальные токи и напряжения, так и их составляющие (свободные и принужденные составляющие).

Задача 4.2.1. На рис. 4.2.1 E = 100 В, L = 10 Гн, R = 20 Ом. Найти ток I и напряжения U_L, U_R после коммутации цепи (при переходе ключа из состояния 1 в состояние 2).

Решение.

1. Дифференциальное уравнение цепи после коммутации

.

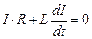2. Характеристическое уравнение R + pL = 0, откуда .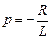

	t 0–	t 0+	t ® ¥
I
UR
UL		–100

3. Таблица начальных условий, из которой видно, что принужденные составляющие всех решений равны нулю.

Тогда решения будут иметь вид

; ; .

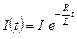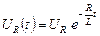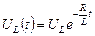Величины I, U_R, U_L находятся из частного решения этих уравнений при t ₀ = t ₀₊:

I (t ₀₊) = I ₀ = 5 A; U_R (t ₀₊) = U_{R 0} = 100 B; U_L (t ₀₊) = U_{L 0} = – 100 B.

Окончательно решения имеют вид

I (t) = 5 e ^{-2 t} A; U_R (t) = 100 e ^{-2 t} B; U_L (t) = – 100 e ^{-2 t} B.

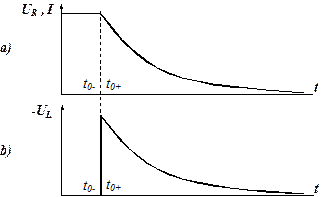
Рис. 4.2.2

4. Графики переходного процесса изображены на рис. 4.2.2а и 4.2.2б

Задача 4.2.2 (для самостоятельного решения). Решить предыдущую задачу при условии, что ключ коммутируется из положения 2 в положение 1.

Можно обратить внимание на тот факт, что характеристическое уравнение (4.2.1) цепи, представленной на рис. 4.1.1, имеет аналогию с выражением полного сопротивления цепи для синусоидального переменного тока в символическом методе:

.

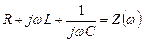Если это выражение приравнять к нулю и оператор jw заменить опера­тором p, получим характеристическое уравнение (4.2.1).

Эту аналогию можно углубить, понимая под оператором p т. н. обобщенную частоту, т. е. частоту, которая изменяется от бесконечности до нуля при развитии во времени переходного процесса, т. е.

.

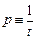В первый момент времени переходного процесса t = 0, p ® ¥, т. е. частота переходного процесса бесконечно велика. Для этого момента времени сопротивление индуктивности pL бесконечно велико, сопротивление емкости 1/pC бесконечно мало. Индуктивность равноценна разрыву цепи, емкость – короткому замыканию.

При нарастании времени переходного процесса частота p переходного процесса падает. В результате сопротивление индуктивности pL падает, сопротивление емкости 1/pC растет. В пределе, при t ® ¥, сопротивление индуктивности становится равным нулю, сопротивление емкости – бесконечно большой величине. Такая частотная интерпретация, аналогично законам коммутации, может быть использована для анализа начальных условий задачи о переходном процессе и составления таблицы.

Таким образом, цепь на рис. 4.1.1 при переходном процессе обладает сопротивлением:

.

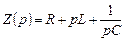В общем случае для сложных цепей может быть составлена система характеристических уравнений, например, по методу контурных токов (или узловых потенциалов). Определитель этой системы, приравненный к нулю, будет характеристическим уравнением системы

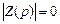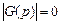, . (4.3.2)

Таким образом, формально ха­рак­теристическое уравнение есть полное сопротивление цепи на частоте p, приравненное нулю. Пользуясь этим выводом и анало­гией с символическим методом, можно не составлять систему дифференциальных уравнений, а сразу начинать решение задачи с составления системы характе­рис­тических урав­нений. Продемонстрируем выше­сказанное решением задачи с использованием метода контур­ных токов.

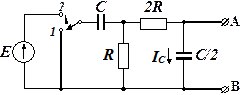Рис. 4.3.1

Задача 4.3.1. В цепи, представ­ленной на рис. 4.3.1, найти ток I_C и напряжение U _AB при переклю­чении ключа из положения 1 в положение 2.

Решение. Составим опреде­ли­тель сопротивлений по методу контурных токов и приравняем его к нулю (см. свойства 1–3 в § 1.3.4):

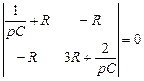; откуда ,

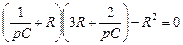решим полученное уравнение

;

; .

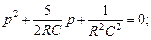
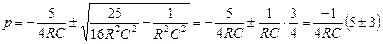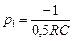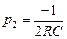Таким образом, решение для тока будет иметь вид

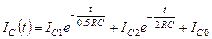. (4.3.3)

Решение для напряжения найдем интегрированием решения (4.3.3):

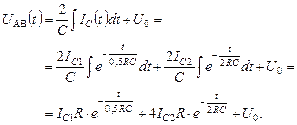(4.3.4)

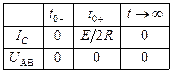
Составим таблицу начальных условий, пользуясь частотной интерпрета­цией переход­ного процесса. Из таблицы видно, что при­нуж­денные составляющие тока и напряжения I_{C 0} и U ₀равны нулю. Найдем решения уравнений (4.3.3) и (4.3.4) для момента :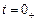

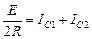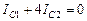; , откуда ; .

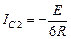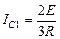Окончательное решение для тока

.

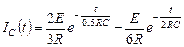Решение для напряжения имеет вид

.

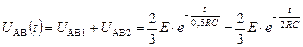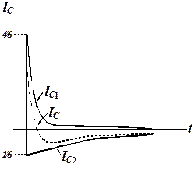
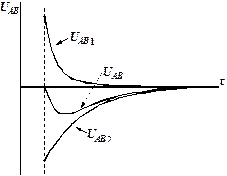
Рис. 4.3.2 Рис. 4.3.3

На рис. 4.3.2 представлен переходный процесс для тока 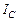, на рис. 4.3.3 – для напряжения U _AB.

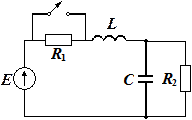Рис. 4.3.4

Задача 4.3.2. На схеме рис. 4.3.4 R ₁ = R ₂ = 10⁵ Ом, L = 160×10^-6 Гн, E = 100 В, C = 160×10^-12 Ф. Найти токи и напряжения после замыкания ключа.

Решение. 1.Найдем характеристи­ческое уравнение

,

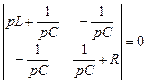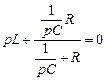, откуда .

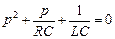Корни характеристического уравнения

,

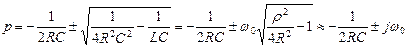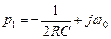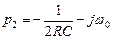, . (4.3.5)

2. Составим таблицу начальных условий:

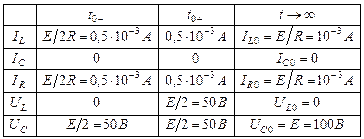
3. В общем виде решение для токов и напряжений:

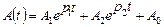. (4.3.6)

Однако так как корни характеристического уравнения комплексно сопряжены, сопряжены не только p ₁ и p ₂, но и коэффициенты A ₁ и A ₂; в результате решение можно представить как

.

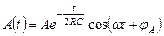4. Найдем напряжение и ток конденсатора:

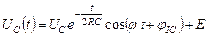; (4.3.7)

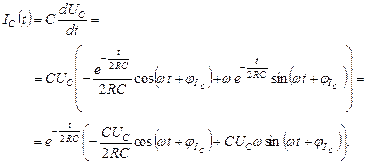(4.3.8)

Решим уравнение (4.3.8) для момента t = 0₊:

;

;

; .

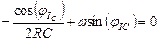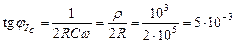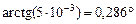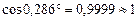Решим уравнение (4.3.7) для момента :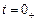

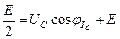, откуда .

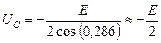Окончательно напряжение на емкости:

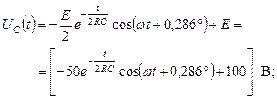
Ток через емкость:

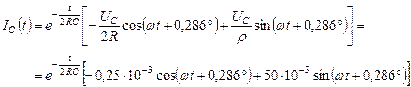A.

Ток через резистор R ₂:

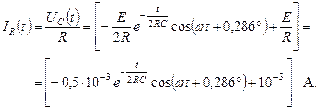
Ток индуктивности I_L можно найти из уравнения Кирхгофа:

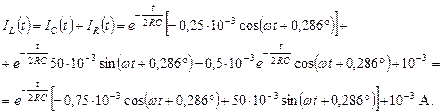
Напряжение на индуктивности так же найдем из уравнения Кирхгофа:

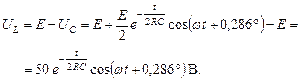
На рис. 4.3.5а и 4.3.5б представлены в качестве приме­ра графики переходных процес­сов напряжений на катушке индуктивности и на конден­саторе (здесь и далее графики получены с помощью модели­рующей программы Work Bench).

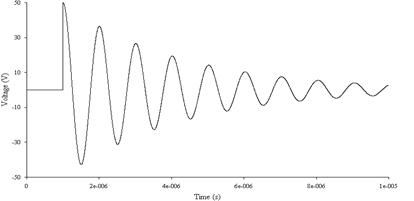
Рис. 3.4.5а

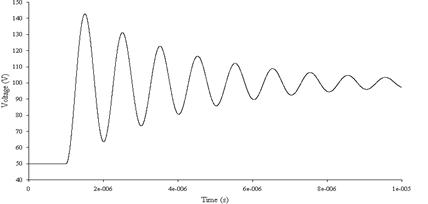
Рис. 3.4.5б

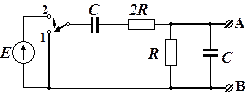Рис. 4.3.6

Задача 4.3.3 (для само­сто­я­тельного решения). На рис. 4.3.6 изображена схема фильтра, назы­ваемого мостом Вина. Найти напряжение U _AB при переклю­че­нии ключа из положения 1 в положение 2. Изобразить график переходного процесса.

Задача 4.4.1. Рассмотрим вариант переходного процесса в RC – цепи при подключении ее к источнику переменной э.д.с. На рис. 4.4.1 E = 50sin(wt– 30°) B, R = 20 Ом, X_C = 35 Ом, C = 90×10^-6 Ф, f = 50 Гц. Найти I (t), U_R (t), U_C (t).

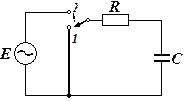Рис. 4.4.1

Решение.

1. Характеристическое уравнение

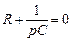, откуда

.

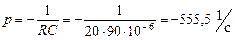2. До подключения к источнику все напряжения и токи в цепи равны нулю. После коммутации, в момент t ₀₊

;

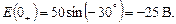
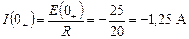	t 0–	t 0+:	t ® ¥
E	–25 B	–25 B	50 e ^-^30^° B
I		–1,25 A	1,24 e ^j30^° A
UC			43,4 e ^–60^° B
UR		–25 B	24,8 e ^j30^° A

.

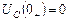Занесем эти данные в таблицу начальных состояний.

3. По окончании переходного процесса (при t ® ¥) в цепи уста­новятся синусоидальный переменный ток и синусоидальные переменные напряжения, которые удобно представить в рамках символического метода:

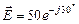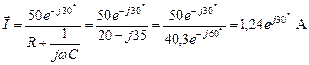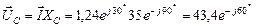B;

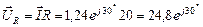; B;

B.

4. Общие решения для тока и напряжений:

I (t) = I _св + 1,24 e^{j 30°};

.

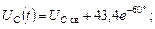
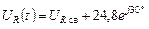Решим эти уравнения для момента времени t = 0₊:

–1,25 = I _св + 1,24 sin30° = I _св + 1,24×0,5 = I _св + 0,62, откуда

I _св = – 0,62 – 1,25 = – 1,87 A;

0 = U_{C св} + 43,4 sin(–60°) = U_{C св} – 43,4×0,866 = U_{C св} – 37,6, откуда

U_{C св} = 37,6 B;

–25 = U_{R. св} + 24,8 sin30°= U_{R. св} + 24,8×0,5 = U_{R. св} + 12,4, откуда

U_{R. св} = –25 – 12,4 = –37,4 B

Подставим результаты в уравнения для тока и напряжений:

I (t) = –1,87 e ^{-555,5 t} + 1,24 sin(w t + 30°);

U_C (t) = 37,6 e ^{-555,5 t} + 43,4 sin(w t – 60°);

U_R (t) = – 37,4 e ^{-555,5 t} + 24,8 sin(w t + 30°).

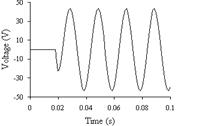
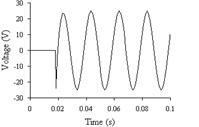
Рис. 4.4.2а Рис. 4.4.2б

5. На рис. 4.4.2а и 4.4.2б изображены графики переходных процессов U_R и U_C соответственно.

Задача 4.4.2. В какой момент (при какой фазе источника) необходимо разомкнуть ключ K в схеме цепи на рис. 4.4.1, чтобы при размыкании ключа отсутствовал переходный процесс? Предполагается, что в цепи имеет место установившийся процесс, т. е. свободные составляющие тока и напряжений отсутствуют.

Решение. Очевидно, что переходного процесса можно избежать, если ключ разомкнуть в момент, когда напряжение на конденсаторе равно нулю. В этот момент реактивная энергия в цепи отсутствует:

U_{C 0} sin (wt – 60°) = 0; Þsin (wt – 60°) = 0; Þ wt – 60°= 0; откуда

w t = 60°.

Составим уравнение Кирхгофа для контура:

E sin (wt – 30°) = U_{R 0} sin (wt + 30°) + U_{C 0} sin (wt – 60°);

подставим в него wt = 60°:

E sin (60° – 30°) = U_{R 0} sin (60° + 30°) + U_{C 0} sin (60° – 60°);

E sin 30° = U_{R 0} sin 90° + U_{C 0} sin 0°.

Таким образом, если отключить источник при фазе 30°, в цепи будет отсутствовать переходный процесс.

Надо заметить, что (аналогично) если при этой фазе источника подключить к нему цепь, переходный процесс также будет отсутствовать, т. е., в токе и напряжениях цепи будут отсутствовать свободные составляющие.

Рис. 4.4.3

Задача 4.4.3 (для самостоятельного реше­ния). На рис. 4.4.3 L = 160×10^-6 Гн, E = 20sin (w t – 30°), C = 160×10^-12 Ф, r = 10 Ом, частота генератора, совпа­дает с резонансной частотой колебательного кон­ту­ра. Найти ток контура и напряжения на индуктивности и емкости.

Дата добавления: 2014-12-24