Операторный метод анализа переходных процессов

Решение дифференциальных уравнений, как правило, осуществляется путем их алгебраизации тем или иным методом.

В классическом методе результатом алгебраизации дифференциального уравнения является характеристическое уравнение, которое является как бы схемой цепи, представленной в алгебраической форме. Если мы имеем характеристическое уравнение, по нему можно изобразить схему цепи, и наоборот: по схеме цепи можно составить характеристическое уравнение.

Другим примером алгебраизации дифференциального уравнения может быть символический метод, где алгебраизация достигается заменой функции времени ее изображением – комплексной амплитудой.

Преобразование Лапласа, аналогично символическому методу, позволяет, путем перехода от функции времени к функции комплексной частоты p алгебраизировать дифференциальное уравнение. Подобно символическому методу решение разбивается на три этапа:

1. Переход от функции времени к функции комплексной частоты p с помощью преобразования Лапласа

.

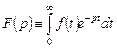2. Решение задачи в функциях комплексной частоты, т. е. нахождение токов и напряжений в цепи как функций комплексной частоты p.

3. Обратный переход от функций комплексной частоты к функциям времени.

Процесс обратного перехода является наиболее сложным моментом решения задачи. Существует несколько способов перехода от изображения к оригиналу. Наиболее употребляемые из них:

Подгонка уравнения решения под одну из формул соответствия, которые приводятся в справочниках.

Непосредственное применение формулы обратного преобразования Лапласа с использованием теории вычетов.

Использование т. н. формулы разложения.

Осуществим в качестве примера преобразование по Лапласу уравнения последовательного контура, подключенного к источнику э.д.с.:

.

Подвергнем преобразованию Лапласа каждый член этого уравнения:

1. ;

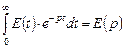2. ;

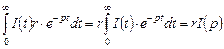3. 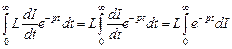. (4.5.1)

далее интегрирование производим по частям:

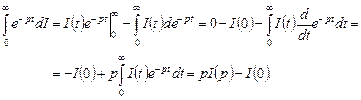
Подставим полученный результат в (4.5.1):

;

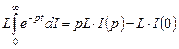4.

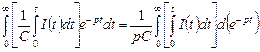
Аналогично возьмем интеграл по частям:

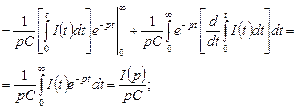
5.

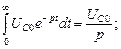
Результирующее изображение дифференциального уравнения примет вид

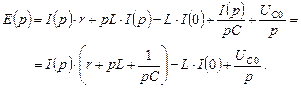(4.5.2)

Как видно, изображение (4.5.2) есть алгебраическое равенство. выражения pL и 1/ pC есть по смыслу индуктивное и емкостное сопротивления в операторном представлении и называются они операторными сопротивлениями. Константы интегрирования L × I (0) и U_{C 0}/ p

Рис. 4.5.1

отображают начальные условия задачи, т. е. тот факт, что в момент времени t _0– в индуктивности протекал ток I (0), а на емкости было напряжение U_{C 0}. Знаки этих э.д.с. таковы, что 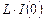всегда совпадает с внешней э.д.с. E (p), а U_{C 0}/ p направлена против э.д.с. E (p).

На рис. 4.5.1 представ­лена прин­ципиальная схема ко­ле­бательного контура в опе­раторном представ­лении, соот­ветствую­щая уравнению (4.5.2).

Найдем изображение тока и нап­ряжений колебатель­ного кон­тура:

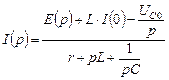. (4.5.3)

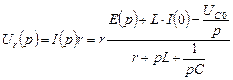. (4.5.4)

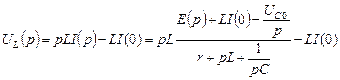. (4.5.5)

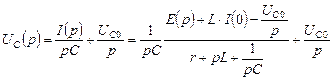. (4.5.6)

Третий этап решения – переход от изображений к оригиналам лучше продемонстрировать на конкретном примере.

Задача 4.5.1. На рис. 4.5.2 r ₁ = r ₂ = 10 Ом, L = 160×10^-6 Гн, C = 160×10^-12 Ф. Источник постоянной э.д.с. E = 2 В. Рассмотреть переход­ный процесс в контуре при размыкании ключа K, найти ток и напряжения, используя операторный метод.

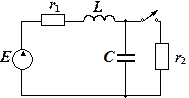Рис. 4.5.2

Решение. В момент размыкания ключа в цепи имели место следующие начальные условия:

.

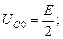
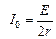Найдем изображение тока и напряжений контура, используя равенства (4.5.3) – (4.5.6), подставив в них началь­ные условия:

.

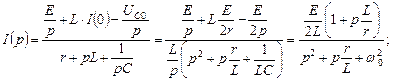
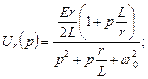
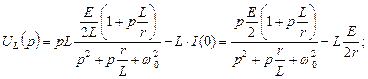
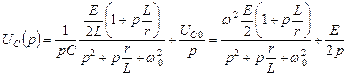Перейдем от изображений к оригиналам, используя формулу разложения (см. приложение 2):

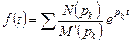, где p_k есть корни многочлена M (p):

;

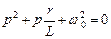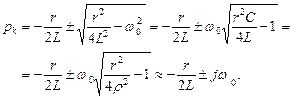
Здесь сделано приближение, учитывающее, что :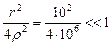

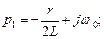
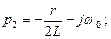
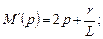
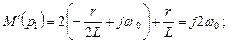
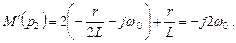
Оригинал тока:

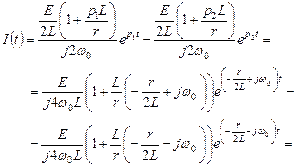
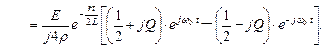
В полученном выражении можно сделать еще одно приближение, если учесть, что Q = 100 >>1/2:

.

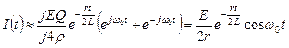Оригинал напряжения на резисторе r:

.

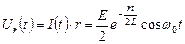Оригинал напряжения на индуктивности проще получить, продиф­фе­рен­цировав выражение оригинала тока. Опуская подробности, приведем ответ:

.

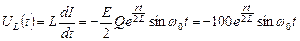Оригинал напряжения на емкости можно найти из уравнения Кирхгофа:

E = U_r + U_L + U_C, откуда

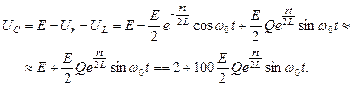
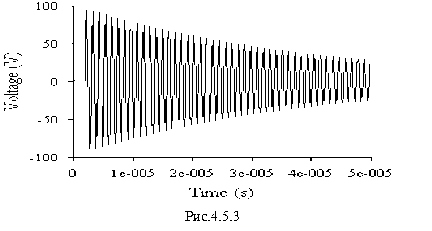
На рис. 4.5.3 в качестве примера изображен график напряжения на конден­са­торе C при переходном процессе.

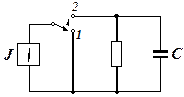Рис. 4.5.4

Задача 4.5.2 (для самостоятельного реше­ния). На рис. 4.5.4 R = 4 кОм, С = 20 мФ. При переводе ключа из состо­яния 1 в состояние 2 величина тока источ­ника J начинает возрастать от нулевого зна­чения по закону J (t) = 2,5 t A. Опреде­лить, каким будет напряжение на резисторе через время t = 0,08 с.

Дата добавления: 2014-12-24