Преобразование звезды в треугольник и треугольника в звезду

В электрических цепях имеют большое распространение структуры из трех ветвей в виде трехлучевой звезды и треугольника. Рассмотрим, в частности, эти фигуры, состоящие из резисторов: звезду сопротивлений и треугольник сопротивлений (рис. 1.3.14).

При расчете электрических цепей часто оказывается целесообразным участок цепи, имеющий структуру звезды сопротивлений, преобразовать в треугольник сопротивлений, или наоборот, что позволяет иногда существенно упростить расчет цепи. Внешние, окружающие фигуру элементы цепи «не замечают» подобных преобразований, ибо потенциалы звезды и треугольника в процессе преобразования остаются неизменными.

Задача 1.3.16 (рис. 1.3.14). Осуществить переход от звезды к треуголь­нику, что означает необходимость выразить резисторы R ₁₂, R ₂₃, R ₁₃ треугольника через величины резисторов R ₁, R ₂, R ₃звезды. Такой переход можно осуществить, используя метод узловых потенциалов.

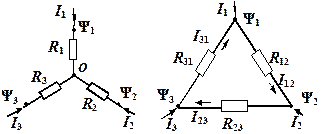
Рис. 1.3.14

Решение. Для звезды (ее единственного узла при потенциале 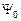) запишем уравнение

I ₁ + I ₂ + I ₃ = 0. (1.3.14.1)

Выразим токи I ₁, I ₂, I ₃ через потенциалы и проводимости резисторов:

I ₁ = (Y₁ ‑ Y₀) g ₁; I ₂ = (Y₂ ‑ Y₀) g ₂; I ₃ = (Y₃ ‑ Y₀) g ₃.

Схема треугольника отличается от схемы звезды отсутствием потенциала Y₀, поэтому в процессе преобразования необходимо избавиться от потенциала Y₀, выразив его через другие потенциалы. Подставим значения I ₁, I ₂, I ₃ в исходное уравнение (1.3.14.1) и решим его относительноY₀:

.

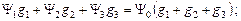
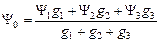Теперь в выражениях для токов I ₁, I ₂, I ₃ можно избавиться от потенциала Y₀. Например, для тока I ₁

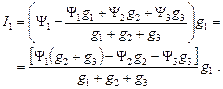(1.3.14.2.)

Выразим теперь ток I ₁ через токи треугольника

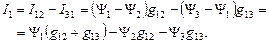(1.3.14.3)

Сравним уравнения (1.3.14.2) и (1.3.14.3). Они состоят из трех членов с потенциалами Y₁, Y₂, Y₃. Полагая, что эти потенциалы одинаковы в обеих схемах, приходим к выводу, что коэффициенты при них так же должны быть равны:

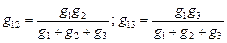. (1.3.14.4)

Аналогично можно найти g ₂₃:

.

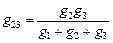Полученные выражения легко запоминаются, если заметить их следующие свойства:

а) в знаменателе всех выражений стоит сумма проводимостей звезды,

б) в числителе стоят проводимости звезды, прилегающие к соответствую­щей проводимости треугольника (см. рис. 1.3.14).

Задача 1.3.17. Осуществить переход от треугольника к звезде, что означает необходимость выразить резисторы звезды через величины резисторов треугольника. Такое преобразование треугольника в звезду можно осуществить следующим образом: выразим, например, выражения (1.3.14.4) через сопротивления:

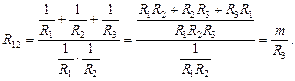(1.3.14.5)

Аналогично 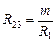; 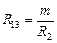, где 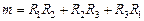, откуда

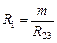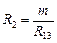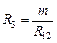; ; . (1.3.14.6)

Подставив (1.3.14.6) в (1.3.14.5), получим

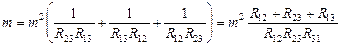,откуда

.

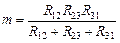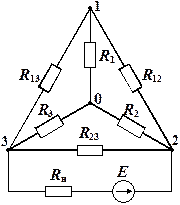Рис. 1.3.15a

Подставив значение m в (1.3.14.6), найдем

,

,

.

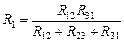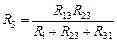Задача 1.3.18 (для самостоятельного реше­ния). На рис. 1.3.15a R _н = R, R ₁ = R ₂ = R ₃ = R, R ₁₂ = R ₂₃ = R ₁₃ = 3 R. Найти ток в нагрузке R _н. Решение рекомендуется осу­ществить путем преобразования звезды резисторов R ₁, R ₂, R ₃ в треугольник резисторов.

Дата добавления: 2014-12-24