Метод, основанный на использовании первого и второго законов Кирхгофа

Принцип наложения и метод наложения

Принцип наложения формулируется следующим образом: ток в какой-либо ветви равен алгебраической сумме токов, вызываемых каждой из э.д.с., имеющихся в цепи. Этот принцип справедлив для всех линейных электрических цепей. Принцип наложения лежит в основе метода расчета, получившего название метода наложения.

Задача 1.3.5. Решим задачу 1.3.1. методом наложения.

Вместо источника E ₂ поставим перемычку и найдем ток в нагрузке:

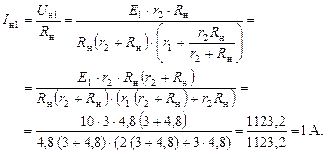
Вместо источника E ₁ поставим перемычку и найдем ток в нагрузке:

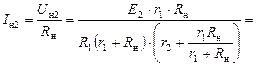
Результирующий ток в нагрузке:

I _н = I _н1 + I _н2 = 2 – 1 = 1 А.

Законы Кирхгофа позволяют найти ток и напряжение в любой ветви цепи, если все элементы цепи известны.

Первый закон Кирхгофа: алгебраическая сумма токов, притекающих к узлу цепи, равна нулю:

I ₁ + I ₂ + I ₃ +×××+ I_N = 0.

Второй закон Кирхгофа: алгебраическая сумма электродвижущих сил и падений напряжений вдоль любого замкнутого контура равна нулю:

E ₁ + E ₂ +× × ×+ E_n + U ₁ + U ₂ +×××+ U_m = 0.

Решение задач сводится к составлению и решению системы уравнений Кирхгофа. Для составления систем уравнений существуют правила, позволяющие составить систему из минимально необходимого числа уравнений, равного числу неизвестных величин.

Первое правило: по первому закону Кирхгофа составляется N–1 уравнений, где N – число узлов в цепи.

Перед составлением уравнений произвольно указываются направления токов в ветвях цепи. Предпочтительно, однако, чтобы направления токов совпадали с направлениями э.д.с. Условно присваиваются знаки величинам токов. Например, если ток входит в узел, то считаем его положительным, если выходит из узла, то отрицательным.

Второе правило: по второму закону Кирхгофа составляется M – (N – 1) уравнений, где M – число ветвей цепи.

Замечание: можно также пользоваться правилом: число уравнений по второму закону Кирхгофа равно числу независимых контуров цепи (неза­ви­си­мый контур – контур, включающий в себя хотя бы одну ветвь, не входящую в предыдущие контуры). Для составления уравнений выбирается направление обхода контуров, определяющее знаки членов уравнений. Удобно придержи­вать­ся определенных правил присвоения знаков членам уравнений. Например:

1) если направление э.д.с. совпадает с направлением обхода контура, присваиваем ему знак «плюс», если нет – знак «минус»;

2) если направление тока в резисторе совпадает с направлением обхода, присваиваем падению напряжения знак «плюс», если нет – знак «минус»;

3) все э.д.с. располагаем по одну сторону знака равенства, все падения напряжения – по другую.

Число уравнений, составленных по первому и второму законам Кирхгофа, должно быть равно числу неизвестных токов ветвей.

Задача 1.3.6 (см. рис. 1.3.5). E ₁ = 10 В, E ₂ = 30 В, r ₁ = 2 Ом, r ₂= 3 Ом, R _н = 4,8Ом. Найти ток и напряжение на нагрузке R _н.

Решение. Схема имеет два узла (1 и 2), и, т. о., число уравнений по первому закону Кирхгофа равно N – 1 = 2 – 1 = 1: I ₁ – I ₂ – I _н = 0.

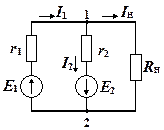Рис. 1.3.5

Число ветвей в цепи три, тогда число уравнений по второму закону Кирхгофа равно M – (N – 1) = 3 – (2 – 1) = 2:

E ₁ + E ₂ = I ₁ r ₁ + I ₂ r ₂;

– E ₂ = – I ₂ r ₂ +I _н R _н.

Полная система уравнений:

I ₁ – I ₂ – I _н = 0;

– E ₂ = – I ₂ r ₂ + I _н R _н;

E ₁ + E ₂ – I ₁ r ₁ – I ₂ r ₂ = 0.

Решение системы:

I _н = I ₁ – I ₂,

I ₁ найдем из второго уравнения, I ₂ – из третьего:

.

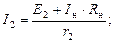
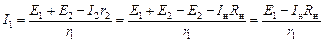Полученные значения I ₁ и I ₂ подставим в первое уравнение:

;

;

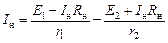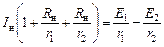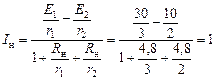А.

Задача 1.3.7. Составить систему уравнений Кирхгофа для нахождения токов в ветвях цепи, изображенной на рис. 1.3.6, полагая, что все величины элементов цепи известны.

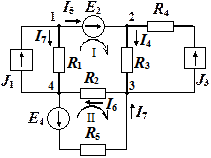Рис. 1.3.6

Решение задачи представим в двух вариантах.

Вариант 1.

Схема имеет четыре узла, следова­тель­но, по первому закону Кирхгофа должно быть три уравнения:

1) J ₁ – I ₂ – I ₅ = 0;

2) I ₅ + J ₃ – I ₄ = 0;

3) I ₄ – I ₇ – J ₃ – I ₆ = 0.

Составление уравнений по второму закону Кирхгофа имеет особенность в связи с наличием в цепи источников тока. Для контуров, включающих в себя источники тока, не могут быть составлены уравнения, так как сопротивление источников тока бесконечно велико. Однако в этом и нет необходимости. Подсчитаем число неизвестных токов в цепи, их оказывается пять (I ₂, I ₄, J ₅, I ₆, I ₇). Следовательно, по второму закону Кирхгофа достаточно составить два уравнения для тех контуров, где отсутствуют источники тока:

4) E ₂ = I ₄ R ₃ +I ₆ R ₂ – I ₂ R ₁;

5) – E ₄ = – I ₇ R ₅ –I ₆ R ₂.

Для цепей, имеющих в своем составе источники тока, можно сделать замечание: составляя уравнения по второму закону Кирхгофа, не следует учитывать ветви с источниками тока.

Вариант 2. Второй вариант решения предполагает предварительную замену в схеме цепи источников тока эквивалентными источниками э.д.с. После преобразования схема принимает вид, изображенный на рис. 1.3.6a.

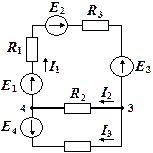Рис. 1.3.6a

Составим систему уравнений:

1) I ₁ – I ₂ + I ₃ = 0;

2) E ₁ + E ₂ – E ₃ = I ₅ (R ₁ + R ₃) + I ₂ R ₂;

3) – E ₄ = – I ₃ R ₅ – I ₂ R ₂.

Где E ₁ = J ₁ R ₁; E ₃ = J ₃ R ₃.

Сравнивая оба варианта решения, можно сделать вывод, что второй вариант предпоч­ти­тельней.

Задача 1.3.8. Составить систему уравнений для цепи, изображенной на (рис. 1.3.7).

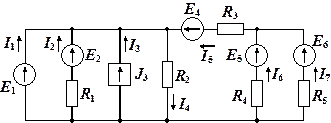
Рис. 1.3.7

Решение. При наличии в цепи ветви с идеальным источником э.д.с. (т. е. ветви с нулевым сопротивлением) составление системы уравнений цепи так же имеет особенность. В ветвях E ₂ R ₁, J ₃ и R ₂, шунтированных идеальным источ­ни­ком э.д.с. E ₁, токи находятся непосредственно, независимо от токов в дру­гих ветвях: .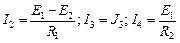

Исключим эти ветви из цепи и для оставшейся части составим систему уравнений:

1) I ₅ + I ₆ + I ₇ = 0,

2) E ₁ – E ₄ – E ₅ = – I ₁ R ₃ – I ₆ R ₄,

3) E ₅ – E ₆ = I ₆ R ₄ – I ₇ R ₅.

Из этой системы уравнений можно найти токи I ₅, I ₆, I ₇ остальных ветвей системы. Ток I ₁ найдется из уравнения I ₁ = I ₄ – I ₂ – I ₃ – I ₅.

Дата добавления: 2014-12-24