Метод контурных токов. Метод контурных токов может рассматриваться как дальнейшее развитие метода, использующего законы Кирхгофа

Метод контурных токов может рассматриваться как дальнейшее развитие метода, использующего законы Кирхгофа. В качестве неизвестных величин в методе используются т. н. контурные токи, т. е. полагают, что в каждом неза­висимом контуре цепи течет свой контурный ток. Это дает возможность огра­ни­читься составлением уравнений только по второму закону Кирхгофа и, т. о., иногда существенно уменьшить число урав­нений системы. Реальные токи ветвей на­хо­дятся суммированием контурных токов. Как будет показано ниже, этот метод имеет еще и то преимущество, что в наибольшей степени возможна матема­тическая формали­за­ция ре­ше­ния системы уравнений.

Рис. 1.3.8

Задача 1.3.9. На рис. 1.3.8 E ₁ = 10 В, E ₂ = 30 В, r ₁ = 2 Ом, r ₂= 3 Ом, R _н = 4,8Ом. Найти ток и напряжение на нагрузке R _н, пользуясь методом контурных токов.

Решение. По второму закону Кирхгофа необходимое число уравнений определяется условием M – (N – 1), где M – число ветвей, N – число узлов, или число независимых контуров цепи:

1. E ₁ + E ₂ = I ₁₁ r ₁ + (I ₁₁ – I ₂₂) r ₂;

2. – E ₂ = (I ₂₂ – I ₁₁) r ₂ +I ₂₂ R _н.

Решение системы уравнений приводит к нахождению контурных токов I ₁₁, I ₂₂, а через них и токов ветвей:

I ₁ = I ₁₁, I ₂ = I ₁₁ – I ₂₂, I _н = I ₂₂.

Приведем систему к следующему виду:

1. (r ₁ + r ₂) – r ₂ I ₂₂ = E ₁ + E ₂;

2. – r ₂ I ₁₁ + (R _н + r ₂) I ₂₂ =– E ₂.

Представим систему уравнений в матричной форме:

. (1.3.4.1)

Система уравнений обладает определенными свойствами, учитывая которые можно существенно облегчить ее решение.

1. В диагональ матрицы сопротивлений, называемую главной, входят т. н. полные сопротивления контуров:

(r ₁ + r ₂) = R ₁₁ – сопротивление первого контура;

(r ₂ + R _н) = R ₂₂ – сопротивление второго контура.

2. Остальные члены матрицы со знаком минус есть т. н. взаимные сопротивления, т. е. смежные сопротивления между контурами:

– r ₂ = R ₁₂ – сопротивление между первым и вторым контурами,

– r ₂ = R ₂₁ – сопротивление между вторым и первым контурами.

3. Система симметрична относительно главной диагонали:

R ₁₂ = R ₂₁.

В правой части уравнений имеем сумму электродвижущих сил каждого контура.

E ₁ + E ₂ = E ₁₁ – сумма э.д.с. первого контура,

– E ₂ = E ₂₂ – сумма э.д.с. второго контура.

Э.д.с. берется со знаком «плюс», если его направление совпадает с направлением обхода контура, и «минус», если его направление встречное.

Замечание. Все качества системы уравнений, перечисленные в пунктах 1 – 4, имеют место при условии, что направление обхода контуров одинаково.

В общем виде система уравнений произвольного порядка теперь может быть представлена в виде

[ R ] × [ I ] = [ E ] или

.

Решение системы может быть осуществлено, например, с помощью правила Крамера:

.

Здесь | R | есть определитель системы, | D _NN | – определитель, полученный путем замены в определителе | R | N-го столбца столбцом матрицы электродвижущих сил.

Продолжим решение задачи, подставив численные значения в уравнения (1.3.4.1):

;

;

;

; ; .

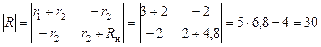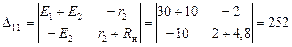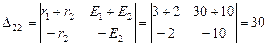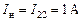Задача 1.3.10 (рис. 1.3.9). Составить систему уравнений по методу контурных токов.

Решение. Поскольку для контуров с источниками тока уравнения не составляются, система будет иметь два уравнения:

1. (I ₁₁– J ₁) R ₁ +(I ₁₁+ J ₃) R ₂+(I ₁₁– I ₂₂) R ₄ = E ₂;

2. I ₂₂ R ₅ + (I ₂₂– I ₁₁) R ₄ = – E ₄.

Приведем к каноническому виду

1. I ₁₁(R ₁ + R ₂+ R ₄) – I ₂₂ R ₄ = E ₂+ J ₁ R ₁ – J ₃ R ₂;

2. – I ₁₁ R ₄+ I ₂₂(R ₄ + R ₅) = – E ₄.

Приведем к матричному виду

.

Источники тока (помно­жен­ные на шунтирующие их сопро­тив­ления) оказались в правой части системы уравнений вместе с электро­движу­щими силами, т. о. как бы автомати­чески произошла замена источников тока на источники э.д.с. Следова­тельно, в методе контурных токов нет необходимости предва­ри­тельно осуществлять преобра­зо­ва­ние источников тока в источники э.д.с.

Рис. 1.3.9 Рис. 1.3.10

При известном навыке, используя вышеприведенные правила 1 – 4, систему уравнений цепи можно сразу представить в матричной форме, минуя промежуточные выкладки.

Задача 1.3.11 (для самостоятельного решения). Составить систему уравнений в матричной форме для цепи, представленной на рис. 1.3.10.

Дата добавления: 2014-12-24