Лекция 1. Понятия о группе, кольце и поле. Поле комплексных чисел

Дурак советует: носи этот Кодекс постоянно с собой.

Он поможет тебе в самый критический момент

твоей жизни — когда вдруг закончится

туалетная бумага.

www.e-puzzle.ru

[1] Фрагмент стихотворения воспроизводится по памяти. Имя автора в ней, к сожалению, не сохранилось. — Прим. автора.

[2] Настоящая глава является стенограммой дополнительного занятия, до недавнего времени проводимого лишь изустно. В ней содержится множество цитат, не выделенных, тем не менее, как цитаты, так как текст этот изначально не предназначался для печати. Исправить это положение сейчас уже не представляется возможным из-за полной их ассимиляции с текстом авторским ( честно говоря, автор просто забыл, что именно здесь не его ). В связи с этим выражаем благодарность всем « поневоле » принявшим участие в подготовке данной главы, а именно ( кого удалось вспомнить ): Наполеону Хиллу, Уэйну Дашру, Игорю Калинаускасу, Василию Гачу, Рону Хаббарду, Т. и Дж. Пауяллам, Ричарду Карлсону, Роберту Грисвалду.

[3] Фрагмент стихотворения воспроизводится по памяти. Имя автора в ней, к сожалению, не сохранилось. — Прим. автора.

[4] Дураку плевать на то, что некоторые нелепости, им говоренные, уже кто-то говаривал ранее:

— Вы полагаете, это вами придумано? — смеется он. — ошибаетесь, это сказал дурак, живущий в вас. А значит — Я.

Определение. Пусть - множество. Бинарной алгебраической операцией * на множестве называется соответствие, при котором каждой паре элементов из множества сопоставляется единственный элемент этого же множества.

Определение. Множество с заданной на нем бинарной алгебраической операцией * называется группоидом (алгебраической системой) и обозначается .

Определение. Группоид называется полугруппой, если

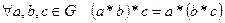(ассоциативность).

Определение. называется моноидом, если

1. 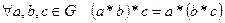(ассоциативность),

2. 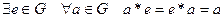(элемент называется нейтральным элементом относительно *)

Определение. называется группой, если

1. (ассоциативность),

2. 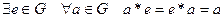(элемент называется

нейтральным элементом относительно *)

3. , где - нейтральный

элемент (элемент называется обратным элементом к

элементу ).

Определение. называется абелевой группой, если

1. (ассоциативность),

2. 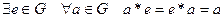(элемент называется

нейтральным элементом относительно *)

3. , где -нейтральный элемент

(элемент называется обратным элементом к элементу ).

4. (коммутативность).

Нейтральный элемент единственный. Обратный элемент к элементу единственный.

Определение. Пусть теперь - непустое множество, на котором заданы две алгебраические операции и ×. Обозначение . называется кольцом, если

1. - абелева группа (называемая аддитивной группой

кольца),

2. - полугруппа (называемая мультипликативной

полугруппой),

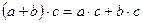3. операции и × связаны дистрибутивными законами

и .

Определение. Если является моноидом, называется кольцом с единицей.

Определение. Кольцо называется коммутативным, если .

Определение. Если 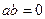при и в кольце , то называется левым, а 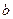правым делителем нуля. В коммутативном кольце говорят просто о делителях нуля. Если в кольце нет делителей нуля, то называется кольцом без делителей нуля.

Определение. Коммутативное кольцо с единицей и без делителей нуля называют целостным кольцом (кольцо целостности или область целостности).

Определение. Кольцо называется полем, если

1. - абелева группа,

2. - абелева группа,

3.

Дата добавления: 2014-12-24