Лекция 2. Операции над комплексными числами. Алгебраическая и тригонометрическая форма комплексного числа

Записьв виде 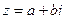называется алгебраической формой комплексного числа. Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости .

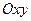Плоскость называется комплексной, если каждому комплексному числу 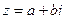ставится в соответствие точка плоскости 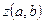, причем это соответствие взаимно однозначное. Ос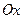и и 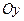, на которых расположены действительные числа 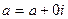и чисто мнимое числа 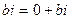, называются соответственно действительной и мнимой осями. С каждой точкой 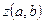комплексной плоскости связан радиус вектор этой точки 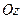, длина которого 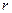называется модулем комплексного числа и обозначается : .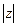

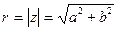Угол 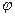, образованный радиус-вектором 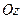с осью 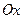, называется аргументом комплексного числа и обозначается 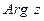. Из значений 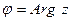выделяется главное значение 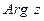, удовлетворяющее условию 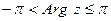. Очевидно, что 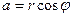, 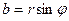. Следовательно, комплексное число 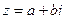можно представить в ви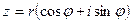де , где 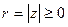, 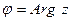. Это представление называется тригонометрической формой комплексного числа.

При сложении (вычитании) комплексных чисел их радиус-векторы складываются (вычитаются) по правилу параллелограмма.

Модуль произведения (частного) двух комплексных чисел равен произведению (частному) модулей этих чисел, а его аргумент – сумме (разности) аргументов этих чисел.

Так как при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 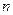, известную как формула Муавра: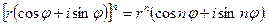

Геометрически умножение числ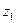а на 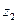означает изменение длины радиус-вектора 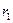(или ) в (или 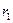) раз и его поворот вокруг точки против часовой стрелки на угол (или ).

Дата добавления: 2014-12-24