Суждение об устойчивости системы по ЛЧХ прямого канала и обратной ЛЧХ канала обратной связи

Об устойчивости замкнутой САУ можно судить по расположению ЛЧХ встречно-параллельных соединяемых звеньев, не прибегая к непосредственному построению ЛЧХ САУ в разомкнутом состоянии.

Доказано, что любая замкнутая САУ представляется в виде встречно-параллельного соединения звеньев (рисунок 5.18).

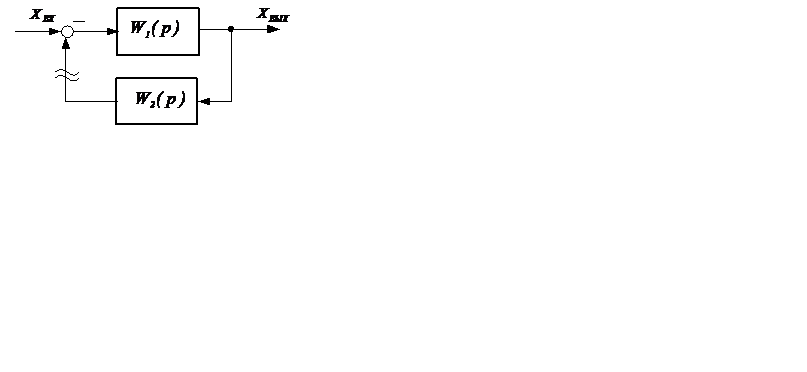Передаточная функция разомкнутой системы равна

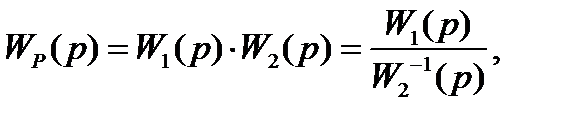(5.34)

Комплексный коэффициент передачи

Рисунок 5.18

. (5.35)

Для построения логарифмических амплитудно-фазовых характеристик системы автоматического управления необходимо построить характеристики L₁(ω), φ₁(ω), L₂^-1(ω), φ₂^-1(ω) и определить поправки. Как известно

L_P(ω)= L₁(ω)- L₂^-1(ω),

φ_P(ω)= φ₁(ω)- φ₂^-1(ω), (5.36)

то есть ординаты между ЛАЧХ и ЛФЧХ прямого и обратного каналов представляют собой значения соответственно ЛАЧХ и ЛФЧХ системы в разомкнутом состоянии.

Пересечения ЛАЧХ прямого и обратного каналов происходят при частоте среза, то есть, L_P(ω) =0,

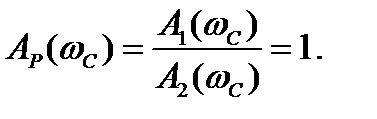
Если при L_P(ω)=0, φ_P(ω)=180 ^°, то поправочная ордината А_П=0

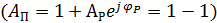и, следовательно, L_П(ω)=-∞, то есть L(ω) при ω=ω_С бесконечно возрастает. Таким образом, применительно к рассмотренному соединению звеньев критерий устойчивости Найквиста может быть сформулирован следующим образом.

Система автоматического управления в замкнутом состоянии устойчива, если в точке пересечения логарифмических амплитудно-частотных характеристик прямого канала и обратной амплитудно-частотной характеристики канала обратной связи разность фаз между логарифмической фазо-частотной характеристикой прямого канала и обратной логарифмической фазо-частотной характеристикой канала обратной связи меньше 180° (рисунок 5.19).

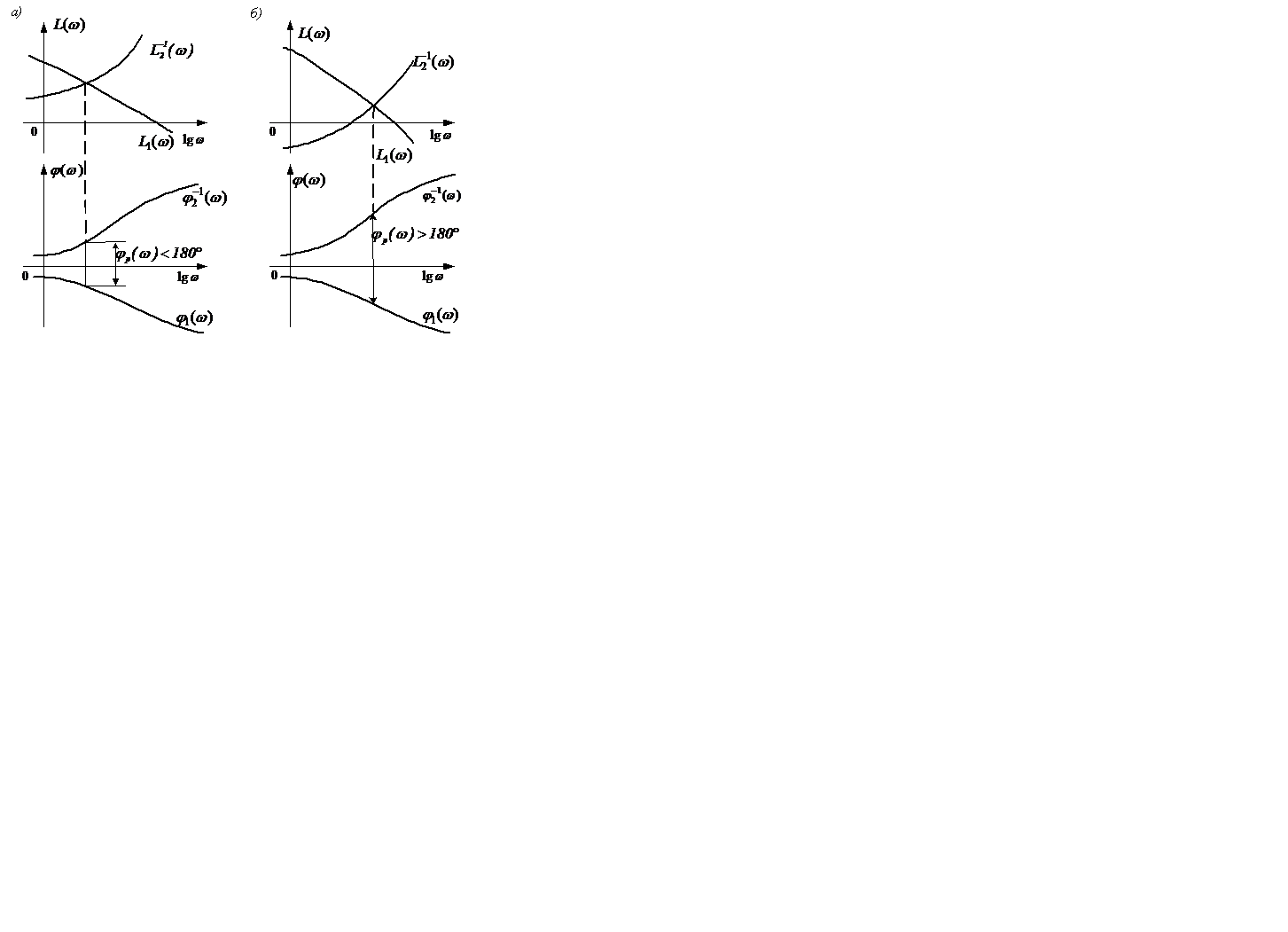
Рисунок 5.19 – Устойчивая а) и неустойчивая б) САУ

Пример 5.12. Определить устойчивость замкнутой системы вида

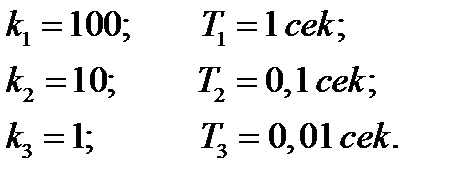Пусть

Построим ЛАФЧХ системы в разомкнутом состоянии, то есть такой системы:

Определим параметры, необходимые для построения ЛАЧХ и ЛФЧХ

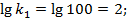
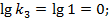
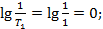
Построенные по этим данным ЛАЧХ и ЛФЧХ показаны на рисунке 5.20.

Вывод: поскольку , то система в замкнутом состоянии неустойчива.

Мы рассмотрели одноконтурную замкнутую систему. Если исследуется поведение многоконтурной САУ, то проверяют устойчивость всех контуров. А именно, строится φ₁^-1, φ₂^-1 . Определяется, устойчив ли первый контур. Если контур устойчив, находится результирующие ЛАЧХ и ЛФЧХ этого контура. Строится L₁,. L₂ следующего контура и т.д. Если какой-то контур неустойчив или обладает плохими качествами переходного процесса, то вводят корректирующие устройства с тем, чтобы система имела желаемые показатели регулирования.

Дата добавления: 2014-12-25