Частотный критерий устойчивости Найквиста

Для исследования устойчивости усилителей с обратной связью Найквист в 1932 г. предложил критерий устойчивости, основанный на анализе частотных характеристик системы. Для исследования устойчивости замкнутой системы управления, согласно этому критерию, необходимо знать амплитудно-фазовую частотную характеристику разомкнутой системы, которую можно получить аналитически, так и экспериментально. Последнее обстоятельство выгодно отличает рассматриваемый критерий устойчивости от ранее изложенных.

Пусть дана система

Рисунок 5.6 – Замкнутая САУ

В разомкнутом состоянии передаточная функция системы равна

. (5.24)

Так как 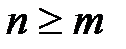, то порядок полинома 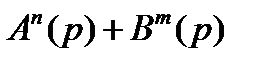и полинома 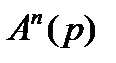одинаков.

Передаточная функция замкнутой системы равна

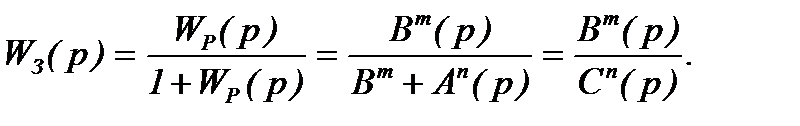
(5.25)

Рассмотрим отдельно знаменатель

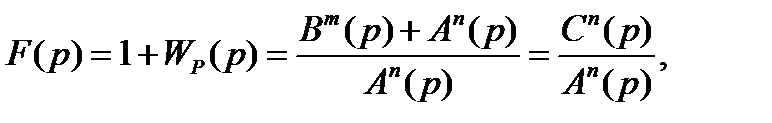
(5.26)

где 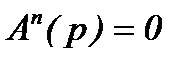- характеристическое уравнение разомкнутой системы;

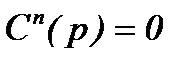- характеристическое уравнение замкнутой системы.

Т.е. характеристические уравнения разомкнутой и замкнутой систем связаны общим уравнением.

Для получения АФЧХ системы положим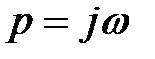

,

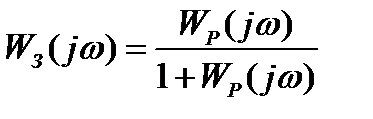где 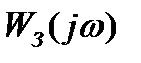- АФЧХ замкнутой САУ,

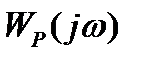- АФЧХ разомкнутой САУ.

Рассмотрим три случая состояния разомкнутой системы: устойчива, неустойчива и находится на грани устойчивости.

1 случай - рассмотрим случай, когда разомкнутая система устойчива.

Если САУ в разомкнутом состоянии устойчива, то по критерию Михайлова

Если потребовать, чтобы система в замкнутом состоянии была устойчива, то должно удовлетворяться равенство

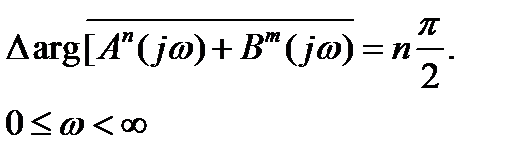
При этом из (5.26) следует, что

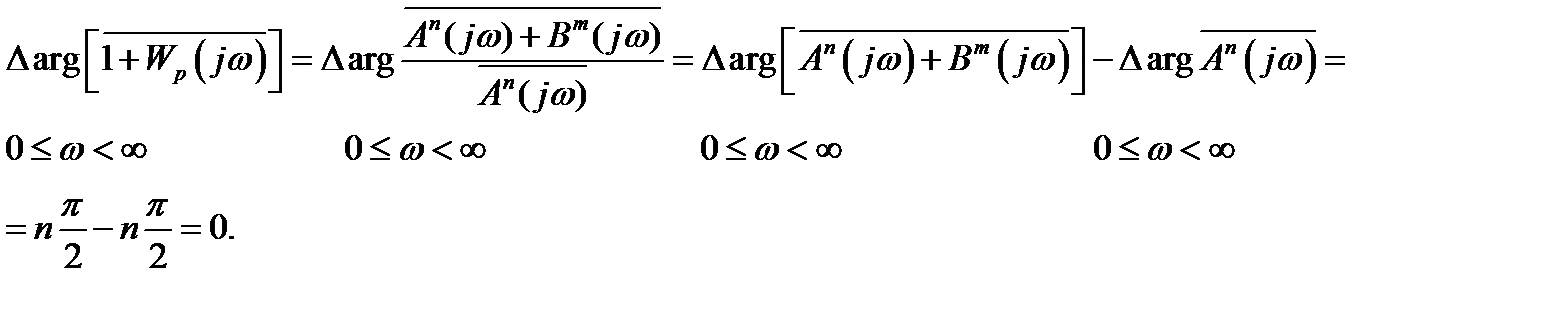
(5.27)

Таким образом, система автоматического управления устойчива, если (и только если) изменение аргумента F(jω) при изменении ω от 0 до ∞ равно 0, то есть устойчивое состояние означает, что годограф вектора не огибает начало координат комплексной плоскости.

Рисунок 5.7 – Годографы устойчивой (а) и неустойчивой (б) систем

На рисунке 5.7 показаны два годографа 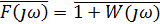: а) соответствует устойчивой системе, так как он не охватывает точку (0, j); б) - неустойчивой, так как он охватывает точку (0, j).

Удобно рассматривать ту же кривую, но для вектора - поскольку годограф есть АФЧХ разомкнутой системы, для этого, очевидно, нужно перенести мнимую ось вправо на 1. Поскольку F(jω) отличается от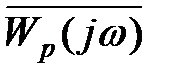

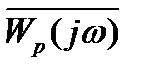на +1, то условие можно получить непосредственно для характеристики

(рисунок 5.7).

Рисунок 5.7

Приведём формулировку критерия Найквиста для этого случая.

Если система управления устойчива в разомкнутом состоянии, то для устойчивости замкнутой системы автоматического управления необходимо и достаточно, чтобы при изменении 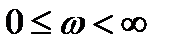годограф амплитудно-фазовая частотной характеристики (АФЧХ) системы в разомкнутом состоянии не охватывал точку с координатами .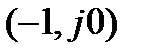

2 случай - система в разомкнутом состоянии неустойчива, то есть характеристическое уравнение 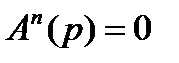имеет q корней, лежащих в правой полуплоскости комплексной плоскости корней.

Рассуждая аналогично устойчивой системе, по принципу приращения аргумента характеристического вектора 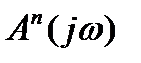в данном случае для не устойчивой системы равно

. (5.28)

Для устойчивой замкнутой системы по-прежнему выполняется равенство

.

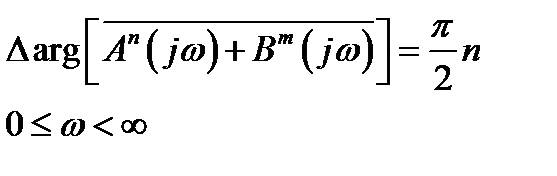Таким образом, в соответствии с (5.27) приращение аргумента равно

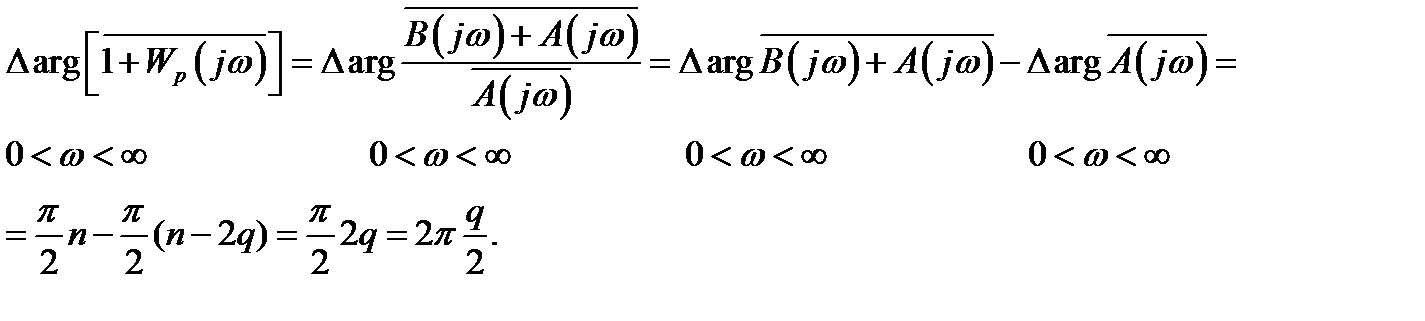(5.29)

То есть при неустойчивой системе в разомкнутом состоянии, имеющей q корней в правой полуплоскости, система в замкнутом состоянии будет устойчивой, если годограф вектора 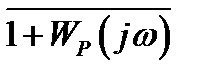при изменении частоты от 0 до 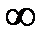огибает в положительном направлении начало координат 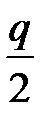раз (рисунок 5.8).

Рисунок 5.8 – Годографы устойчивой (а) и неустойчивой (б) САУ

Аналогично предыдущему: если перенести ось ординат в точку 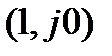, то вместо годографа 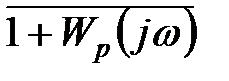можно рассматривать лишь 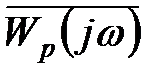, то есть годограф АФЧХ в разомкнутом состоянии (рисунок 5.9).

Рисунок 5.9

Тогда окончательная формулировка критерия Найквиста в этом случае имеет вид.

Если реальная система в разомкнутом состоянии неустойчива и имеет q корней в правой полуплоскости, то в замкнутом состоянии система автоматического управления устойчива, если годограф АФЧХ системы в разомкнутом состоянии 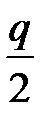раз охватывает в положительном направлении точку с координатами .

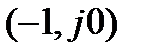3 случай – система в разомкнутом состоянии находится на грани устойчивости. Передаточная функция системы в разомкнутом состоянии

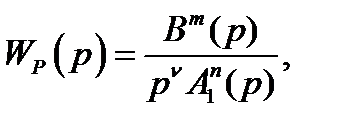(5.30)

где 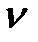-число нулевых корней характеристического уравнения системы в разомкнутом состоянии;

В^m(p), A₁ⁿ(p) – полиномы от р, причём А₁ⁿ(p) не имеет нулей в правой полплоскости и на мнимой оси.

В случае, когда САУ в разомкнутом состоянии имеет 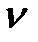нулевых корней

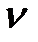( интегрирующих звеньев) анализ устойчивости замкнутой САУ можно вести аналогично случаю устойчивой САУ в разомкнутом состоянии. Для этого условно положим нулевые корни лежащими в левой (устойчивой) полуплоскости корней и численно равными 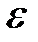. Тогда по критерию Найквиста, для устойчивых САУ в разомкнутом состоянии замкнутая САУ устойчива, если годограф ЛФЧХ САУ в разомкнутом состоянии не огибает точку с координатами 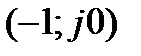(рисунок 5.10,а).

Устремим теперь 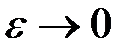, тогда реальная АФЧХ САУ в разомкнутом состоянии будет дополняться частью окружности бесконечно большого радиуса, начинающейся с положительной действительной полуоси (рисунок 5.10,б).

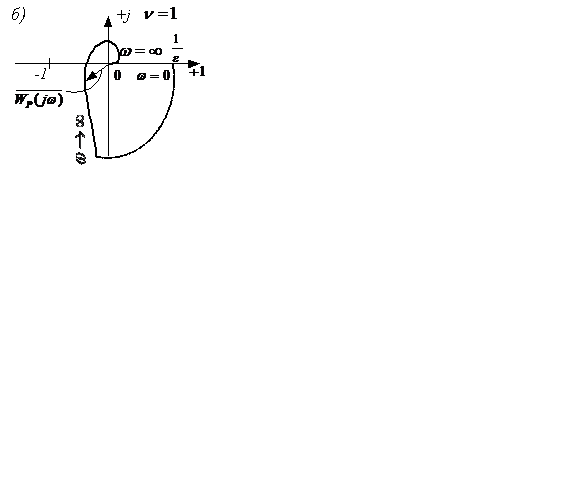
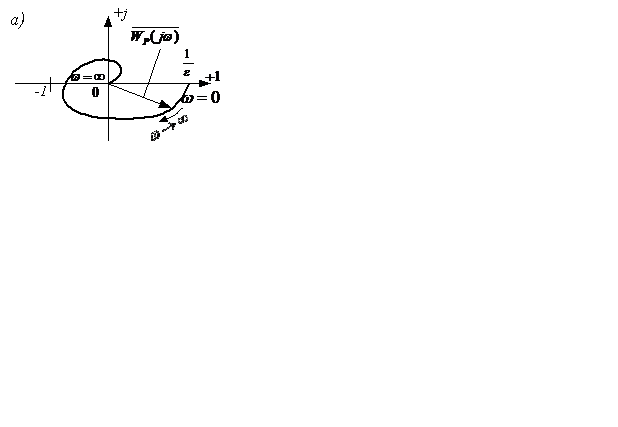
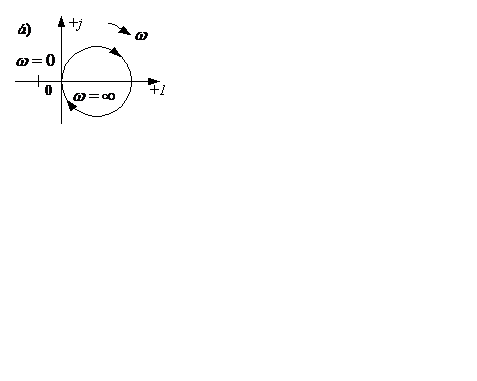
Рисунок 5.10

Таким образом, критерий Найквиста может быть сформулирован следующим образом:

Если САУ в разомкнутом состоянии имеет нулевых корней, то замкнутая САУ устойчива, если годограф АФЧХ в разомкнутом состоянии дополняется окружностью бесконечно большого радиуса, начинающейся с положительной полуоси и проходящей через квадрантов, не огибает точку с координатами .

Пример 5.6. Определить устойчивость следующей САУ

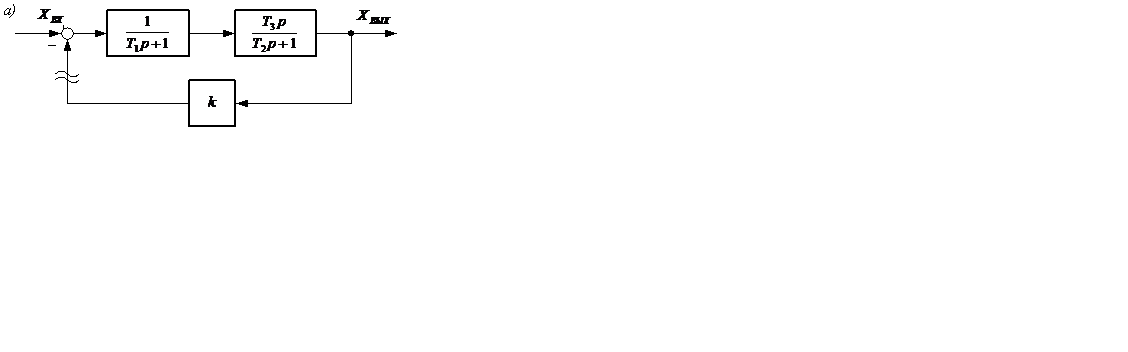
Рисунок 5.10 – Система (а) и её годограф АФЧХ (б)

Реально такой структурной схеме (рисунок 5.10, а) может соответствовать система Г-Д (генератор-двигатель) с отрицательной обратной связью по току.

Передаточная функция разомкнутой САУ равна

.

Получим АФЧХ, заменим

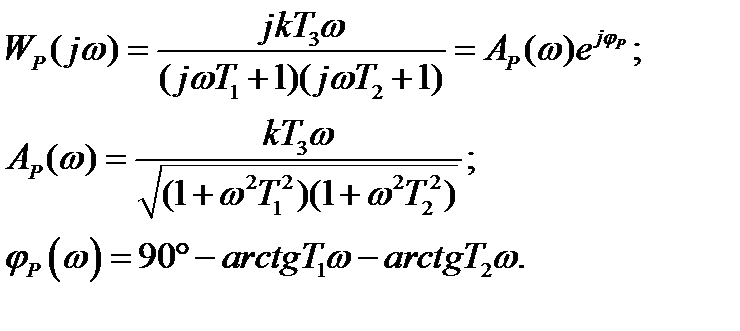
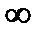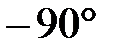Не приводя построения годографа АФЧХ отметим, что при изменении от 0 до изменяется от до через 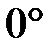(рисунок 5.10,б). При любых значениях постоянной времени k_ОС АФЧХ разомкнутой системы не проходит через точку 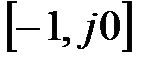, то есть такая система всегда устойчива. Иначе говоря, система с общим порядком интегрируемости равным 1 всегда устойчива (система нулевого порядка тем более устойчива).

Пример 5.7. Определить устойчивость САУ вида (рисунок 5.11, а)

Рисунок 5.11 – Система (а) и её годограф АФЧХ (б)

Так как система имеет интегральное звено, то она относится к разряду астатических САУ.

Передаточная функция разомкнутой системы

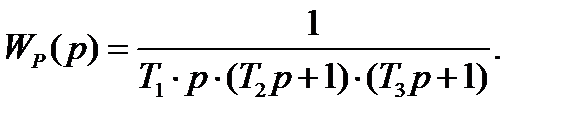
Её АФЧХ получается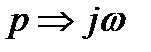

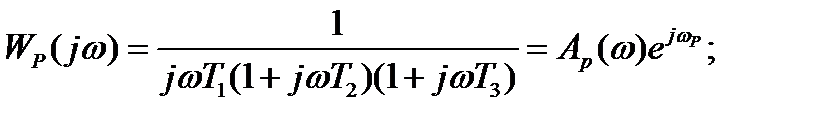
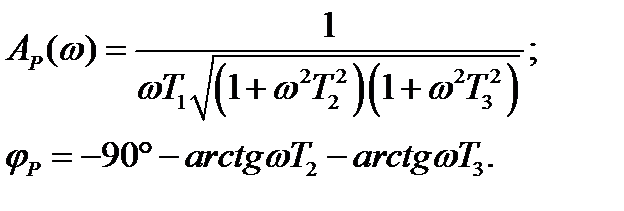
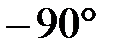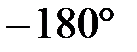Годограф АФЧХ проходит от через до 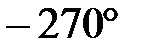при изменении 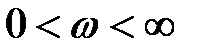, то есть по 3 и 2 квадранту комплексной плоскости. Система может быть устойчивой и неустойчивой.

Для конкретности положим Т₁ = 0,03 сек; Т₂ = 0,02 сек; Т₃ = 0,01 сек. В этом случае

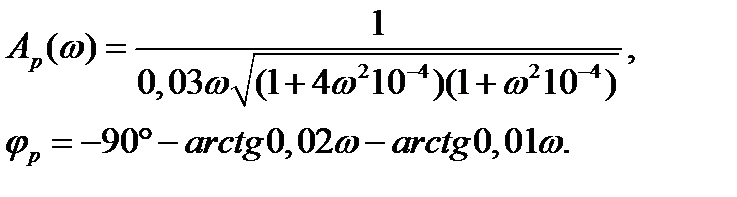
Составим таблицу

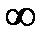
		3,24	1,52	0,52	0,42	0,105
	-90°	-107°	-123°	-138°	-162°	-198°	-270°

Вывод: годограф АФЧХ не охватывает точку 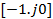, поэтому САУ в замкнутом состоянии система устойчива.

Дата добавления: 2014-12-25