Рассчитать угол сноса

Поступательное движение водной массы в морях и океанах называется течением. Элементами течения являются его скорость и направление. Направление течения получает свое название по той точке горизонта, к которой оно движется, например, на северо-запад, на 105° и т. д. Это хорошо выражается мнемоническим правилом: «течение идет из компаса». Направление течения принято показывать в градусах, а иногда — в румбах. Скорость течения выражают в узлах (числом миль в час), или в кабельтовых в час, или в метрах в секунду. В различных районах Мирового океана скорости течений могут колебаться от 0,3—0,5 до 4—5 и более миль в час (уз).

Перемещения корабля, происходящие под воздействием собственных движителей, а также под влиянием ветра, как установлено в предыдущих параграфах, совершаются относительно воды. Но так как вода сама перемещается в определенном направлении с определенной скоростью, то абсолютное перемещение корабля, т. е. его перемещение относительно берега, дна моря и навигационных опасностей, является результатом сложения двух движений: движения корабля Vл (с черточкой наверху) относительно воды и движения v T (c черточкой) самой воды:

V = Vл + v T (все буквы с черточками на самом верху, как на рисунке внизу слева, - векторы). (175)

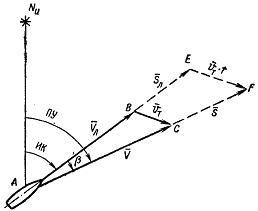Фактическое перемещение корабля происходит по линии АС, которая называется линией пути (рисунок слева).
Задача учета течения сводится к решению треугольника АВС, в котором:
Vл — вектор скорости перемещения корабля относительно воды (скорость по лагу или по оборотам); при отсутствии дрейфа он направлен вдоль диаметральной плоскости корабля, т. е. по курсу;
v T — вектор скорости течения;
V — вектор скорости абсолютного перемещения корабля относительно земной поверхности (дна моря).
Этот треугольник носит название навигационного треугольника или треугольника скоростей. Вектор V иногда называют вектором истинной скорости, но правильнее называть его вектором путевой скорости, а его абсолютную величину путевой скоростью, подчеркивая тем самым, что речь идет о скорости перемещения корабля по линии пути и что вследствие возможных ошибок в учете течения она может быть весьма далека от истинной.

Вместо навигационного треугольника часто решается подобный ему треугольник перемещений АЕF (рисунок слева вверху), в котором:
Vл * t = Sл - расстояние, пройденное кораблем относительно воды по лагу или по оборотам гребных винтов; при отсутствии дрейфа оно прокладывается всегда по линии курса;
v T * t = sт — перемещение водной среды, относительно которой лагом измеряется пройденное кораблем расстояние;
Vл * t + v T * t = S - абсолютное перемещение корабля относительно земной поверхности, дна моря, навигационных опасностей; оно происходит по линии пути.

При решении этих треугольников применяются следующие термины.
Путевой угол (путь корабля) ПУ — угол, который составляет линия пути с направлением истинного меридиана; как и истинный курс, он отсчитывается всегда по часовой стрелке от 0 до 360°.
Угол сноса b — угол между линией курса и линией пути на течении.
Из рисунка вверху слева видно, что эти величины и истинный курс корабля связаны между собой соотношением

ПУ = ИК + b (176)

Когда корабль сносится течением вправо (ПУb больше, чем ИК), угол сноса b считается положительным; при сносе влево — отрицательным.

При учете течения приходится решать следующие основные задачи.

Задача 1.
Заданы истинный курс корабля, его скорость по лагу (по оборотам), направление и скорость течения.
Найти путь и путевую скорость корабля.
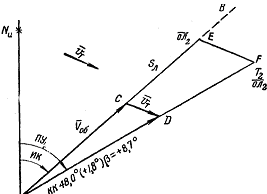Задача решается следующим образом (рисунок слева). От исходной точки А счисления прокладывается линия истинного курса АВ. По этой линии раствором циркуля, равным скорости хода корабля по лагу Vл или по оборотам гребных винтов Vоб, откладывается отрезок АС, изображающий вектор скорости перемещения корабля относительно воды. Из конца этого вектора — точки С — по направлению течения в том же масштабе откладывается вектор скорости течения v T. Отрезок АD изображает геометрическую сумму вектора скорости перемещения корабля относительно воды и вектора скорости течения, т. е. вектор путевой скорости V.
Линия АD есть искомая линия пути корабля с учетом течения, по которой при отсутствии дрейфа и ошибок счисления будет происходить фактическое перемещение корабля. Эта линия проводится на карте несколько толще, чем линия курса, но не толще, чем линии меридианов и параллелей карты. Проведя линию пути, следует, не сдвигая параллельной линейки, приложить к ней транспортир и измерить путевой угол ПУ (угол, который линия пути составляет с меридианом карты). Затем по формуле

b = ПУ - ИК (177)

Вдоль линии пути надписываются компасный курс, поправка компаса (в скобках) и угол сноса b. От непосредственного измерения углов сноса на карте следует воздерживаться, поскольку при измерении с помощью транспортира малых углов возможны большие ошибки.

Задача 2.
Заданы линия пути, по которой должно происходить перемещение корабля (лидия створа, ось фарватера), скорость хода корабля, скорость и направление течения.
Найти, какой курс должен быть назначен, чтобы абсолютное перемещение корабля происходило по заданной линии пути.
Эта задача, обратная только что рассмотренной, сводится к нахождению такого направления вектора скорости перемещения корабля относительно воды Vл, чтобы вектор путевой скорости V удовлетворял равенству

V = Vл + v T

и был направлен вдоль заданной линии пути. Для этого следует от исходной точки А (рисунок слева) провести заданную линию пути АF и (из той же исходной точки А) в избранном масштабе отложить вектор скорости течения v T. 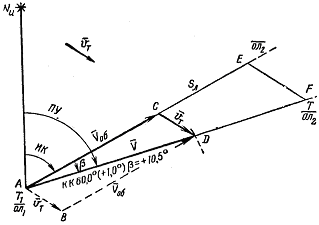Из его конца — точки В — раствором циркуля, равным в том же масштабе скорости хода корабля по лагу Vл (или по оборотам гребных винтов Vоб) сделать засечку на линии пути. Найденную точку D соединить с помощью параллельной линейки с точкой В прямой линией и затем из точки А провести параллельную ей прямую АЕ. Линия АЕ и есть искомая линия истинного курса. Не сдвигая параллельной линейки, надо приложить к ней транспортир и измерить угол, который она составляет с меридианом карты— истинный курс корабля ИК. Если отсутствует дрейф, расчет курса, который должен быть назначен рулевому, производится по формуле
КК = ИК - ΔК.
Угол сноса b течением, как и в предыдущем случае, не измеряется на карте, а рассчитывается по формуле b = ПУ — ИК.

Для контроля правильности расчетов следует проверить, выполняется ли векторное равенство (175) и условие (176):

ПУ = ИК + b = КК + ΔК + b.

Задача 3.

Нанесение счислимой точки на карту.

Эта задача решается построением треугольника перемещений, подобного треугольнику скоростей. Необходимо помнить, что всегда с помощью лага (по оборотам винтов) определяется расстояние, проходимое кораблем относительно воды. Следовательно, независимо от того, каким способом строился треугольник скоростей, необходимо рассчитать пройденное кораблем расстояние по лагу Sл (или по оборотам Sоб = Vоб*t) и отложить его по линии курса. Через полученную таким образом вспомогательную точку Е (см. рисунки вверху) провести прямую ЕF, параллельную вектору скорости течения, до пересечения с линией пути. Точка на линии пути и будет искомым счислимым местом корабля. Возле вспомогательной точки Е на линии курса надписывается только отсчет лага; возле счислимой точки F на линии пути — дробью момент времени и отсчет лага.
Если направление течения близко к направлению линии курса (течение встречное или попутное), этот способ оказывается весьма неточным. В таких случая, отложив по линии курса пройденное расстояние по лагу или по оборотам, из полученной таким образом точки Е следует по направлению течения отложить вектор v T (T2 — T1); его конец и обозначит счислимую точку F.

Задача 4.

Дата добавления: 2014-12-25