Основні характеристики функції

1. Функция 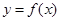, визначена на множині 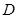, називається парною, якщо 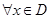виконуються умови 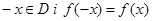; непарної якщо 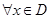виконується умови .

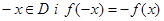Графік парної функції симетричний щодо осі 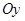, а непарної – щодо початку координат.

2. Нехай функція 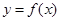визначена на множині 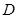і нехай 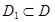. Якщо для будь-яких значень 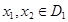аргументів з рівності 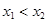випливає нерівність: 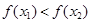, то функція називається зростаючою на множині ; 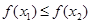, то функція називається неспадною на множині ; 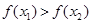, то функція називається спадною на множині 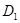; 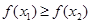, то функція називається незростаючою на множині .

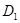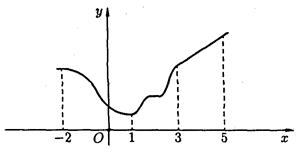
Рис.100

Зростаючі, незростаючі, спадні і неспадні функції на множині 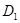називається монотонними на цій множині, а зростаючі і спадні – строго монотонними. Інтервали, в яких функція монотонна, називається інтервалами монотонності. На малюнку (вище) функція строго монотонна на (-2; 1) і (3; 5); монотонна на (1; 3).

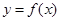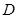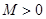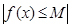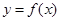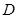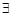
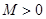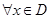
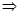
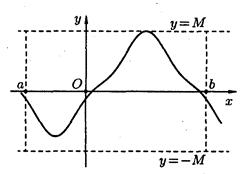
3. Функцию , визначену на множині , називають обмеженою на цій множині, якщо існує таке число , що для всіх виконується нерівність (короткий запис: , , називається обмеженою на , якщо : 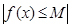. Звідси випливає, що графік обмеженої функції лежить між прямими 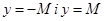(див. рис.101).

Рис.101

4. Функція 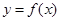, визначена на множині 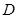, називається періодичною на цій множині, якщо існує таке число 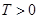, що при кожному значення 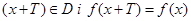. При цьому число 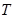називається періодом функції.

14. Числові послідовності. Границя числової послідовності та її геометричний зміст.

Під числовою послідовністю 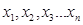… розуміється функція

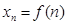(15.1)

задана на множині 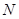натуральних чисел. Стисло послідовність позначається у вигляді 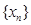або 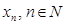. Число 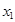називається першим членом (елементом) послідовності, 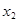- другим, 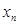- загальним або n-м членом послідовності.

Частіше всього послідовність задається формулою його загального виду члена. Формула (15.1) дозволяє обчислити будь-який член послідовності по номеру n, по ній можна відразу обчислити будь-який член послідовності.

Так, рівність

,

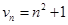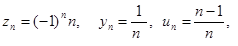
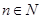
задають відповідно послідовності

=

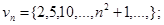
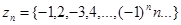
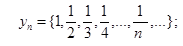
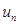Послідовність 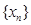називається обмеженою, якщо існує таке число 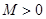, що для будь-кого 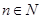виконується нерівність

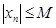
В окремому випадку послідовність називається необмеженою. Легко бачити, що послідовност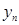і і 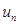обмежені, а 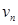і 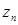– не обмежені.

Послідовність 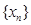називається зростаючою (не спадною), якщо длябудь-кого n виконується нерівність 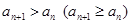. Аналогічно визначається спадна (е зростаюча) послідовність. Всі ці послідовності називаються монотонними послідовностями. Послідовност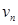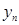і , і 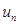монотонні, а 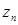- не монотонна.

Якщо всі елементи послідовності 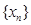рівні одному і тому ж числу з, то її називають постійною.

Дата добавления: 2014-12-26