Інтегрування тригонометричних виразів

Інтегрування диференціального бінома

Інтеграли типу 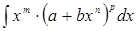(названі інтегралами від диференціального бінома), де 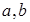– дійсні числа; 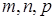– раціональні числа, беруться, як показав Чебишoв П.А., лише у разі, коли хоча б одне з чисел 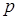, 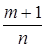або 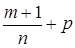є цілим.

Раціоналізація інтеграла в цих випадках здійснюється наступними підстановками:

1) якщо 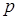- ціле число, то підстановка 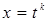, де 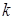– найменше спільне кратне знаменників дробів 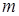і ;

2) якщо 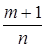- ціле число, то підстановка 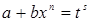, де 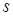- знаменник дробу .

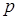3) якщо 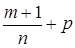- ціле число, то підстановка 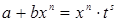, де 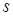- знаменник дробу .

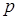У всій решті випадків інтеграли типу 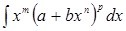не виражаються через відомі елементарні функції, тобто не «беруться».

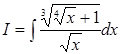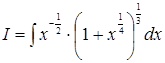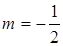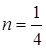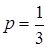
Приклад 8. Знайти інтеграл . Оскільки то , , 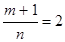. Тому робимо підстановку . Таким чином,

.

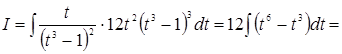
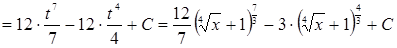Інтеграли типу 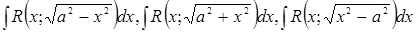зводяться до інтегралів від функцій, раціонально залежних від тригонометричних функцій, за допомогою наступних тригонометричних підстановок: 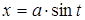для першого інтеграла; 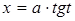для другого інтеграла; 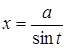для третього інтеграла.

Приклад 6. Знайти інтеграл .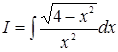

 Покладемо 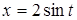, , 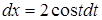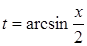. Тоді

.

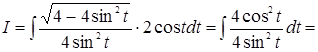
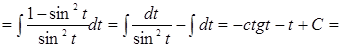
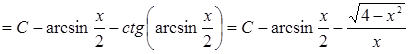
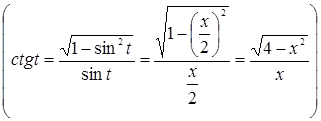63. Визначений інтеграл. Його геометричний зміст.

Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі.

Геометричний зміст цього визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.

Нехай на відрізку задана неперервна функція 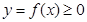. Фігура, обмежена зверху графіком функції 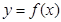, а знизу — віссю Ох, збоку — прямими 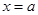і 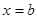, називається криволінійною трапецією. Знайдемо площу цієї трапеції.

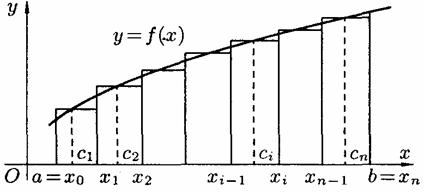
(рис.168)

Для цього відрізок точками , розіб'ємо на частинних відрізків (див. рис. 168). В кожному частинному відрізку 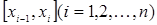візьмемо довільну точку 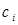і обчислимо значення функції в ній, тобто .

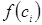Помножимо значення функції 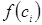на довжину 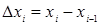відповідного частинного відрізка. Добуток 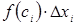дорівнює площі прямокутника з основою 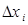і висотою 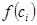. Сума всіх таких добутків

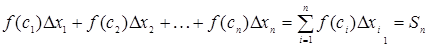
дорівнює площі ступінчатої фігури і приблизно дорівнює площі 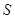криволінійної трапеції:

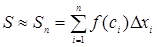, тобто .

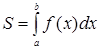Із зменшенням всіх величин 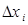точність наближення криволінійної трапеції ступінчатої фігури і точність одержаної формули збільшуються. Тому за точне значення площі 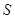криволінійній трапеції приймається границя 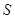, до якої прямує площа ступінчатої фігури 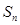, коли 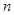необмежено зростає так, що :

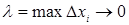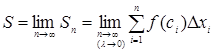, тобто .

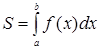Отже, визначений інтеграл від невід’ємної функції чисельно рівний площі криволінійної трапеції.

В цьому і полягає геометричний зміст визначеного інтеграла.

Дата добавления: 2014-12-26