
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Практическое занятие № 17
|
|
|
|
Для развития и контроля владения компетенциями
Задания, решаемые в аудитории
1. Дана функция  , найдите:
, найдите:
а) х и 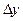 , если
, если 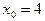 и
и 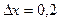 ;
;
б) 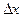 и
и 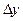 , если х = 2 и
, если х = 2 и 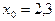 ;
;
в) 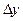 , если х = 1 и
, если х = 1 и 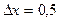 .
.
2. Определите точки разрыва функций и исследуйте ее характер:
а) 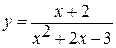 ;
;
б) 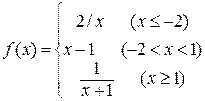 .
.
3. Будет ли непрерывной функция f(х) в точках 1; 2; -1; 0, если
а) 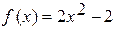 ;
;
б) 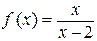 .
.
4. Испытайте функцию 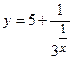 на непрерывность в точке
на непрерывность в точке 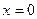 .
.
Задания для самостоятельной работы дома
1. Определите точки разрыва функций и исследуйте ее характер:
а) 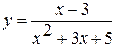 ; б)
; б) 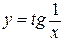 .
.
2. Будет ли непрерывной функция 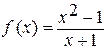 в точках 1; 2; -1; 0?
в точках 1; 2; -1; 0?
3. Приведите примеры функций непрерывных:
а) в любой точке числовой прямой;
б) при всех значениях х, кроме х = 5;
в) при всех значениях х, кроме х = -3; 3 и 8.
4. Какого рода разрыв в точке 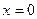 имеет функция
имеет функция 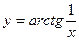 ? Докажите это.
? Докажите это.
Тема занятия «Понятие производной. Правила дифференцирования»
Цель занятия: Введение понятия производной функции с помощью операции предельного перехода, отработка навыков в вычислении производных.
Организационная форма занятия: практикум.
Компетенции, формируемые на занятии: ОК-1, ПК-2.
При формировании названных компетенций в результате изучения дисциплины «Математика» специалист должен знать основные правила дифференцирования; уметь дифференцировать с помощью формул и простейших приемов; владеть методами нахождения производных функций. Формирование у будущих специалистов этой компетенций на занятии предполагает обучение студентов
- сформулировать основные цели выполняемой работы;
- анализировать ситуации и делать выводы;
- вести поиск альтернативных средств и способов решения;
- абстрагировать содержание и выделять существенное;
- осуществлять самоконтроль за работой, объективно оценивать ее результат.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 331; Нарушение авторских прав?; Мы поможем в написании вашей работы!