Методические рекомендации. Вопросы, выносимые на обсуждение

Вопросы, выносимые на обсуждение

Практическое занятие № 49

Тема занятия « Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные, сводящиеся к однородным »

Цель занятия: формирование навыков решения дифференциальных уравнений первого порядка.

Организационная форма занятия: практикум с применением интерактивной доски.

Компетенции, формируемые на занятии:

- способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1);

- способностью и готовностью к анализу медицинской информации при помощи системного подхода, к восприятию инноваций в целях совершенствования своей профессиональной деятельности, к использованию полученных теоретических, методических знаний и умений по фундаментальным естественнонаучным, медико-биологическим, клиническим и специальным (в том числе биохимическим) дисциплинам, в научно-исследовательской, лечебно-диагностической, педагогической и других видах работ (ПК-2, частично: формируется способность использовать методы математического анализа в научно-исследовательской деятельности).

Формирование у будущих специалистов этих компетенций на занятии предполагает обучение студентов

- сформулировать основные цели выполняемой работы;

- анализировать ситуации и делать выводы;

- ставить новые вопросы и видеть проблемы в традиционных ситуациях;

- владеть основными методиками решения учебно-исследовательских задач;

- вести поиск альтернативных средств и способов решения;

- абстрагировать содержание и выделять существенное;

- планировать самостоятельную работу.

1. Основные понятия о дифференциальных уравнениях.

2. Дифференциальные уравнения с разделяющимися переменными.

3. Однородные дифференциальные уравнения первого порядка.

4. Случаи сведения дифференциальных уравнений к однородным.

Для подготовки к занятию дома

11. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

12. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

13. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

14. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

15. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

На занятии по указанию преподавателя

8. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

9. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

10. Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия.

Дома

1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

2. Найдите примеры задач из области естествознания, которые приводят к решению дифференциальных уравнений.

3. Подготовьтесь к компьютерному тестированию по теме «Обыкновенные дифференциальные уравнения первого порядка».

Рекомендуемая литература

[1] глава 13 пп 13.1 - 13.2.

[2] часть 2, глава IV § 1.

[3] глава 10 §§ 60 – 61.

[4] часть III занятие 17.

[5] глава 6 §§ 6.1-6.2.

[6] глава 15 § 1.

[7] глава XV §1.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

1. По общему решению дифференциального уравнения определите порядок исходного уравнения и найти частное отвечающее условиям .

Решение. Так как в общем решении дифференциального уравнения две постоянных, то это решение дифференциального уравнения 2-го порядка. Продифференцируем заданное решение: . Подставляя начальные условия 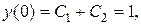, , 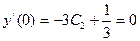в результате получаем систему для определения постоянных, входящих в общее решение: . Решая систему, находим , .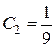

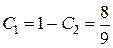Таким образом, - искомое частное решение.

2. Найдите общее решение дифференциального уравнения .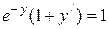

Решение. Данное уравнение является дифференциальным уравнением с разделяющимися переменными. Перепишем его в виде 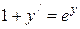, . Далее учитывая, что 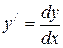, получаем 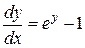, или . Интегрируем последнее уравнение . Вычислим интеграл, стоящий в левой части уравнения:

При нахождении интеграла воспользовались разбиением подынтегральной дроби на элементарные дроби:

.

Тогда решение данного дифференциального уравнения принимает вид 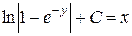, или .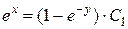

3. Найдите частное решение дифференциального уравнения 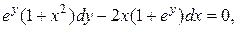отвечающее начальному условию 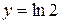при .

Решение. Разделяя переменные, интегрируем уравнение:

.

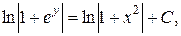
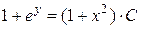Воспользуемся начальными условиями для нахождения константы:

, .

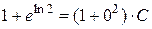Тогда 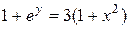- частное решение данного уравнения.

4. Определите вид и найдите общее решение дифференциального уравнения

.

Решение. Данное уравнение является однородным, так как функции и 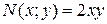являются однородными функциями одного измерения 2. Действительно, и .

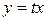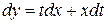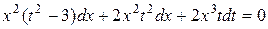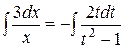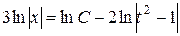Для решения уравнения выполним подстановку , тогда . Следовательно, , , . Получили уравнение с разделяющимися переменными. Разделяя переменные, получим . Далее, , , . Учитывая, что 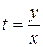, получаем , , 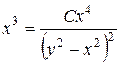. Окончательно имеем - общее решение данного дифференциального уравнения.

5. Покажите, что уравнение можно свести к однородному дифференциальному уравнению первого порядка.

Решение. Так как определитель 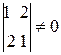, то с помощью подстановки 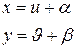, где 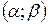решение системы 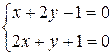, уравнение можно свести к однородному. Решая систему, находим , тогда имеем подстановку 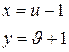, откуда . Переходя к новым переменным в уравнении , получим , 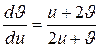. Переписав последнее уравнение в виде , несложно убедиться, что оно однородное. Сделав замену 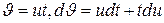, можно привести это однородное уравнение к уравнению с разделяющимися переменными (проделайте эту замену самостоятельно и дорешайте уравнение).

6. Решите уравнение .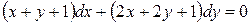

Решение. Так как определитель 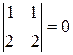, то выполним замену . Тогда , следовательно . Далее 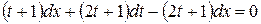, , 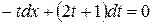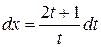. Интегрируем последнее уравнение 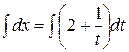и получаем 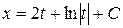. Учитывая, что , находим 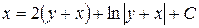- общее решение данного уравнения.

Теоретические задания

Дата добавления: 2014-12-26