
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 2. Определители 2-го порядка и системы линейных уравнений с двумя неизвестными. Определители 3-го порядка. Простейшие правила вычисления определителей. 1 страница
|
|
|
|
ЗАНЯТИЕ 1. Декартовы координаты. Векторы и скаляры. Сложение и вычитание векторов. Действия над векторами, заданными своими проекциями. Скалярное произведение векторов. Направление вектора.
☺ ☻ ☺
Общие формулы:
Пусть  =
=  ,
,  =
=  ;
;  =
= 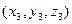 ,
,  =
= 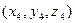 .
.


Тогда: 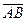 =
= 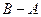 =
=  –
–  =
= 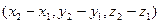 =
= 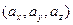 =
=  ,
,
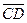 =
= 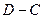 =
= 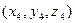 –
– 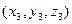 =
= 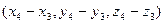 =
= 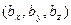 =
=  .
.
Для вектора  :
: 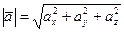 , орт
, орт 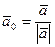 ; проекции вектора на оси координат:
; проекции вектора на оси координат: 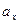 =
= 
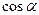 ,
, 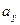 =
= 
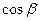 ,
,  =
= 
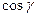 , где
, где  – углы с осями координат
– углы с осями координат 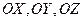 ;
; 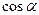 =
=  ,
, 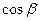 =
=  ,
, 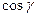 =
= 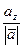 . Также:
. Также: 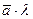 =
= 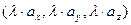 .
.
Пусть имеем векторы:  =
= 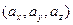 и
и  =
= 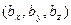 . Для любых вещественных чисел
. Для любых вещественных чисел  и
и 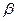 линейная комбинация векторов
линейная комбинация векторов  и
и  записывается в виде:
записывается в виде:
 =
= 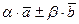 =
= 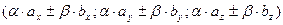 =
=  .
.
Скалярное произведение векторов  и
и  , угол между которыми равен
, угол между которыми равен 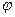 , записывается в виде:
, записывается в виде: 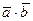 =
=  =
= 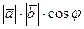 ,
, 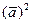 =
= 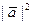 . Также потребуются формулы: вычисление
. Также потребуются формулы: вычисление 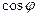 =
= 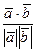 =
= 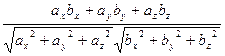 и нахождение проекций:
и нахождение проекций: 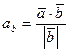 =
=  и
и 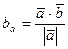 =
= 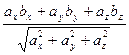 .
.
••• ≡ •••
Пример 1 – 35: Заданы векторы:  = (–1,2,0),
= (–1,2,0), 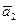 = (3,1,1),
= (3,1,1), 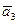 = (2,0,1) и
= (2,0,1) и  =
=  –2
–2 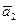 +
+ 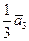 . Вычислить: а)
. Вычислить: а)  и координаты орта
и координаты орта 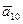 вектора
вектора  ; б)
; б) 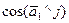 ; в) координату
; в) координату 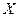 вектора
вектора  ; г)
; г) 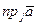 .
.
Решение:
Применяя общие формулы, решим каждую из поставленных задач:
а). Вычислим длину вектора  :
:  =
= 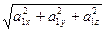 =
= 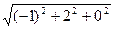 =
= 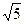 . Вычислим единичный вектор для вектора
. Вычислим единичный вектор для вектора  :
: 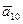 =
=  =
= 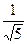 (– 1,2,0).
(– 1,2,0).
б). Вычислим 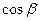 угла между вектором
угла между вектором  и осью
и осью 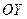 :
: 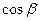 =
= 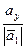 =
= 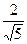 .
.
в). Используя линейные операции над векторами: сложение векторов и умножение вектора на число, вычислим координату вектора 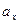 =
= 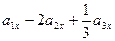 =(– 1)–2·3+
=(– 1)–2·3+ 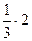 =
= 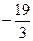 .
.
г). Вычислим проекцию вектора  на ось
на ось 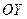 . Если бы мы имели
. Если бы мы имели  и
и 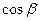 , то можно было бы воспользоваться формулой:
, то можно было бы воспользоваться формулой: 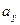 =
= 
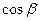 . Мы не имеем ни того ни другого, потому воспользуемся формулой из предыдущего пункта, но для проекции на ось
. Мы не имеем ни того ни другого, потому воспользуемся формулой из предыдущего пункта, но для проекции на ось 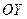 :
: 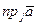 =
= 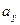 = =
= =  =2–2·1+
=2–2·1+ 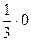 =0.
=0.
Ответ: по пунктам: а) 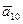 =
= 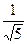 (– 1,2,0), б)
(– 1,2,0), б) 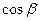 =
= 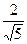 , в)
, в) 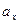 =
= 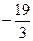 ,
, 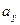 =0.
=0.
Пример 2 – 39: Заданы векторы:  =
= 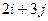 ,
,  =
= 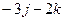 ,
,  =
= 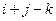 . Вычислить: а) координаты орта
. Вычислить: а) координаты орта 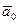 ; б) координат вектора
; б) координат вектора 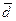 =
= 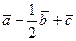 ; в) разложение вектора
; в) разложение вектора 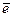 =
= 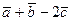 по базису
по базису 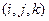 ; г) вычислить
; г) вычислить 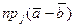 .
.
Решение:
Замечание: предполагается, что все векторы заданы в трёхмерном пространстве с базисом 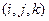 .
.
Применяя общие формулы, решим каждую из поставленных задач:
а). Вычислим длину вектора  :
: 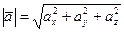 =
= 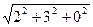 =
= 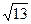 . Вычислим единичный вектор для вектора
. Вычислим единичный вектор для вектора  :
: 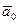 =
= 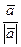 =
= 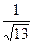 (2,3,0).
(2,3,0).
б). Используя линейные операции над векторами: сложение векторов и умножение вектора на число, вычислим вектор 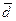 =(2,3,0)
=(2,3,0) 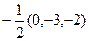 +(1,1,–1) =
+(1,1,–1) = 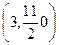 .
.
в). Вычислим вектор 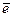 . Задача не отличается от предыдущего пункта:
. Задача не отличается от предыдущего пункта: 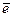 =(2,3,0)+(0,–3,–2) – 2(1,1,–1)= (0,–2,0)=
=(2,3,0)+(0,–3,–2) – 2(1,1,–1)= (0,–2,0)= 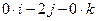 .
.
г). Воспользуемся формулой из предыдущего пункта, обозначив 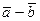 =
= 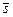 . В таком случае имеем:
. В таком случае имеем: 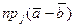 =
= 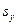 =
= 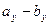 =3–
=3– 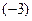 =6.
=6.
Ответ: по пунктам: а) 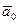 =
= 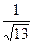 (2,3,0), б)
(2,3,0), б) 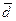 =
= 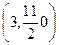 , в)
, в) 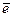 =
= 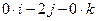 , г)
, г) 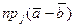 =6.
=6.
Пример 3 – 52: Даны две смежные вершины параллелограмма  :
:  (– 2,6),
(– 2,6),  (2,8) и точка пересечения диагоналей
(2,8) и точка пересечения диагоналей  (2,2). Найти две другие вершины параллелограмма.
(2,2). Найти две другие вершины параллелограмма.
Решение:
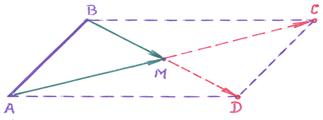 Для решения задачи удобно (хотя не обязательно!) воспользоваться эскизом параллелограмма: точное построение точек в системе координат
Для решения задачи удобно (хотя не обязательно!) воспользоваться эскизом параллелограмма: точное построение точек в системе координат  не требуется!
не требуется!
1. Воспользуемся свойством диагоналей параллелограмма: точкой пересечения 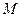 диагонали делятся пополам. Это значит, что можно записать равенства векторов:
диагонали делятся пополам. Это значит, что можно записать равенства векторов:  и
и 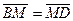 .
.
2. Используя равенства векторов, запишем равенства для точек:
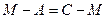 →
→ 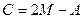 =
=  =(6, – 2);
=(6, – 2);
 →
→ 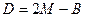 =
= 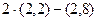 =(2, – 4).
=(2, – 4).
Ответ: вершины:  =(6, – 2);
=(6, – 2); 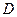 =(2, – 4).
=(2, – 4).
Пример 4 – 55: На оси ординат найти точку 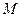 , равноудалённую от точек
, равноудалённую от точек  (1,–4,7),
(1,–4,7),  (5,6,–5).
(5,6,–5).
Решение:
Замечание: для решения задачи удобно (желательно!) воспользоваться эскизом: точное построение точек в системе координат  не требуется: для многих выполнение точного чертежа занимает много времени, кроме того затрудняет восприятие свойства универсальности формул!
не требуется: для многих выполнение точного чертежа занимает много времени, кроме того затрудняет восприятие свойства универсальности формул!
Общие формулы: Пусть:  =
= 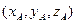 и
и  =
= 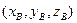 . Учтём правило построения направленного отрезка (геометрического вектора!):
. Учтём правило построения направленного отрезка (геометрического вектора!): 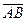 =
= 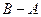 . Тогда длина отрезка:
. Тогда длина отрезка: 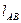 =
= 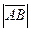 =
= 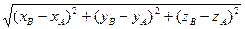 .
.
 1. Обозначим:
1. Обозначим: 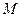 =
=  =
= 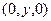 и применим формулу для направленного отрезка:
и применим формулу для направленного отрезка:
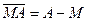 =(1,–4,7)–
=(1,–4,7)– 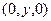 =
= 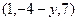 ,
,
 =(5,6,–5)–
=(5,6,–5)– 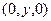 =
= 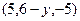 .
.
2. По условию точку 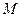 нужно так расположить на оси
нужно так расположить на оси 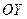 , чтобы расстояния
, чтобы расстояния 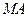 и
и 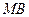 были равными, то есть:
были равными, то есть: 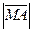 =
= 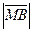 .
.
Мы воспользуемся равноценным ему равенством (так как длина есть величина положительная!): 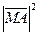 =
= 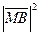 . Применяя формулу для вычисления длины вектора, после несложных алгебраических преобразований, получим уравнение:
. Применяя формулу для вычисления длины вектора, после несложных алгебраических преобразований, получим уравнение:
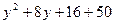 =
= 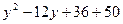 , или:
, или: 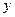 =1.
=1.
3. Получено единственное решение: 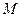 =
=  .
.
Замечание: в общем случае задача может иметь два решения (в том числе совпадающих!) или не иметь ни одного: это зависит от конкретного уравнения 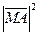 =
= 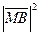 .
.
Ответ: точка: 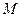 =
=  .
.
Пример 5 – 66: Заданы модули векторов:  =3,
=3, 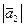 =5. Определить, при каком значении
=5. Определить, при каком значении 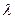 векторы
векторы  =
= 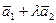 и
и  =
=  будут перпендикулярны.
будут перпендикулярны.
Решение:
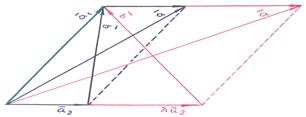 Замечание: для решения задачи удобно (желательно!) воспользоваться эскизом: точное построение точек в системе координат
Замечание: для решения задачи удобно (желательно!) воспользоваться эскизом: точное построение точек в системе координат  не требуется: здесь важно прочувствовать, как параллелограмм превращается в ромб за счёт выбора параметра
не требуется: здесь важно прочувствовать, как параллелограмм превращается в ромб за счёт выбора параметра 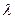 !
!
Общие формулы: учитывая правило графического представления суммы и разности векторов, видим, что векторы  и
и  есть диагонали параллелограмма; из геометрии следует, что за счёт выбора значения должен получиться ромб, то есть
есть диагонали параллелограмма; из геометрии следует, что за счёт выбора значения должен получиться ромб, то есть  =
= 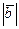 ; мы воспользуемся признаком перпендикулярности векторов:
; мы воспользуемся признаком перпендикулярности векторов: 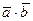 =0.
=0.
Из свойства скалярного произведения следует равенство: 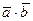 =
= 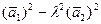 = =
= = 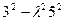 =0. Это значит:
=0. Это значит: 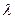 =
= 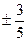 . Графическое изображение ромба в случае
. Графическое изображение ромба в случае 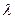 =
= 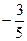 не вызывает затруднения!
не вызывает затруднения!
Ответ: значение: 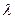 =
= 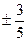 .
.
Пример 6 – 78: Заданы векторы:  =(4,–2,–4),
=(4,–2,–4), 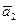 =(6,–3,2). Вычислить: а) скалярное произведение векторов
=(6,–3,2). Вычислить: а) скалярное произведение векторов 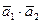 ; б)
; б) 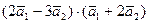 ; в)
; в) 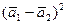 ; г)
; г) 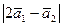 .
.
Решение:
Применяя общие формулы, решим каждую из поставленных задач:
а). Вычислим 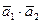 =
= 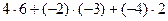 =22.
=22.
б). Вычислим 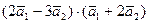 . Можно было бы вычислить векторы
. Можно было бы вычислить векторы  =
= 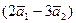 и
и  =
=  , затем воспользоваться формулой
, затем воспользоваться формулой 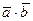 . Мы воспользуемся результатом а): сначала вычислив:
. Мы воспользуемся результатом а): сначала вычислив: 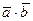 =
=  – использовано распределительное свойство. Вычислим:
– использовано распределительное свойство. Вычислим: 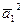 =36,
=36, 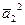 =49 →
=49 → 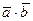 =
= 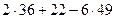 =200.
=200.
в). Вычислим 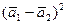 =
= 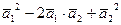 и воспользуемся результатами пунктов а) и б):
и воспользуемся результатами пунктов а) и б): 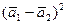 =
= 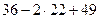 =41.
=41.
г). Вычислим вектор  =
= 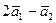 =2(4,–2,–4)–(6,–3,2)=(2,–1,–10) →
=2(4,–2,–4)–(6,–3,2)=(2,–1,–10) →  =
=  .
.
Замечание: можно все вычисления выполнить в координатной форме: определяет автор решения задачи!
Ответ: по пунктам: а) 22, б) 200, в) 41, г)  .
.
Пример 7 – 82: Доказать, что четырёхугольник с вершинами:  (–3,5,6),
(–3,5,6),  =(1,–5,7),
=(1,–5,7),  =(8,–3,–1),
=(8,–3,–1), 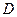 =(4,7,–2) есть квадрат.
=(4,7,–2) есть квадрат.
Решение:
Алгоритм: 1) убедимся, что 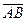 =
= 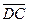 , это значит, что
, это значит, что 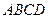 – параллелограмм;
– параллелограмм;
2) проверим равенство сторон 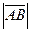 =
= 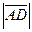 , это значит, что
, это значит, что 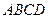 – ромб;
– ромб;
3) убедимся, что 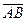 ·
· 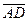 =0, это значит, что
=0, это значит, что 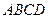 – ромб.
– ромб.
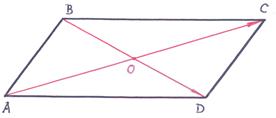 Реализуем принятый алгоритм:
Реализуем принятый алгоритм:
1). Вычислим векторы 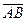 и
и 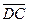 :
:
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 514; Нарушение авторских прав?; Мы поможем в написании вашей работы!