
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 6. Контрольная работа №1. Прием части-1 БДЗ. 5 страница
|
|
|
|
Для случая а):
1). Обозначим прямую линию 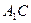 как
как  . Её направляющий вектор
. Её направляющий вектор 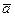 =
= 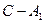 =(1,1,–1). Учитывая, что прямая линия содержит точку
=(1,1,–1). Учитывая, что прямая линия содержит точку  =
= 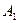 =(0,0,1), записываем каноническое уравнение этой прямой
=(0,0,1), записываем каноническое уравнение этой прямой  :
: 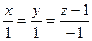 .
.
2). Обозначим прямую линию 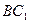 как
как  . Её направляющий вектор
. Её направляющий вектор  =
= 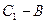 =(0,1,1). Учитывая, что точка
=(0,1,1). Учитывая, что точка 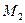 =
=  =(1,0,0), принадлежит
=(1,0,0), принадлежит  , записываем каноническое уравнение этой прямой
, записываем каноническое уравнение этой прямой  :
: 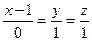 .
.
Для случая б):
1). Так как векторы 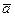 и
и  не параллельны, то
не параллельны, то  и
и  – скрещивающиеся прямые. Расстояние между ними определяется формулой:
– скрещивающиеся прямые. Расстояние между ними определяется формулой: 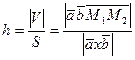 .
.
2). Вычислим:  =
=  x
x  =
= 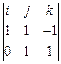 =
= 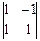 ∙
∙ 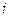 –
– 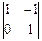 ∙ j +
∙ j + 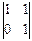 ∙ k =(2,–1,1) →
∙ k =(2,–1,1) → 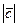 =
= 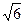 . Вычислим вектор
. Вычислим вектор 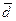 =
=  =
= 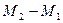 =(1,0,–1). Вычислим:
=(1,0,–1). Вычислим: 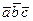 =
= 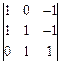 =1. Тогда можем вычислить:
=1. Тогда можем вычислить: 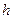 =
= 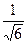 .
.
Для случая в):
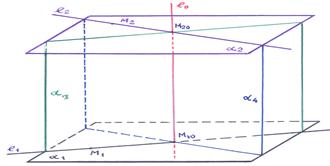 1). Для удобства воспользуемся рисунком, который не привязан к кубу: просто имеются скрещивающиеся прямые
1). Для удобства воспользуемся рисунком, который не привязан к кубу: просто имеются скрещивающиеся прямые  и
и  , и требуется получить уравнение их общего перпендикуляра: обозначен как прямая линия
, и требуется получить уравнение их общего перпендикуляра: обозначен как прямая линия 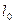 . Обозначим направляющий вектор прямой
. Обозначим направляющий вектор прямой 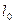 как
как 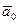 . Он совпадает с вектором
. Он совпадает с вектором  =(2,–1,1).
=(2,–1,1).
2). Теперь наметим укрупнённый алгоритм решения задачи:
▫ строим плоскость 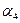 , содержащую точку
, содержащую точку 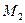 и вектор нормали
и вектор нормали 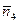 =
= 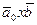 ;
;
▫ находим точку 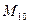 пересечения плоскости
пересечения плоскости 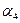 с прямой
с прямой  ;
;
▫ имея точку 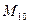 и вектор
и вектор 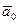 , получаем уравнение для прямой линии
, получаем уравнение для прямой линии 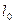 .
.
Реализуем намеченный алгоритм:
3). Вычислим для плоскости 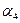 вектор нормали
вектор нормали 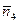 =
= 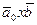 =
= 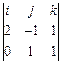 =(–2, –2,2), примем (удобнее) за вектор нормали коллинеарный
=(–2, –2,2), примем (удобнее) за вектор нормали коллинеарный 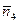 =(1,1,–1). Используя точку
=(1,1,–1). Используя точку 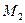 =(1,0,0) и вектор
=(1,0,0) и вектор 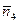 , запишем
, запишем 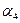 :
: 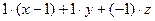 = 0, или
= 0, или 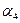 :
: 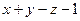 =0.
=0.
4). Из уравнения прямой линии  :
: 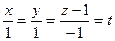 запишем
запишем  =
= 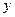 =
= 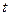 ,
, 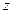 =
= 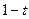 . Из условия
. Из условия 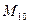 =
= 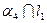 можем записать:
можем записать: 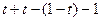 =0, откуда получаем
=0, откуда получаем 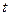 =
= 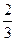 и
и 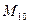 =
= 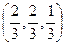 . Теперь можем записать уравнение
. Теперь можем записать уравнение 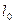 :
: 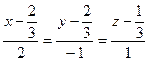 .
.
Замечание: в связи с используемым в задачнике ответом, который выражен как линия пересечения плоскостей 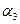 и
и 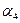 , полезно получить результат:
, полезно получить результат: 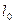 =
= 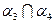 .
.
6). Вычислим для плоскости 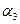 вектор нормали
вектор нормали 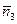 =
= 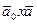 =
= 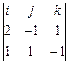 =(0,–3,–3), примем (удобнее) за вектор нормали коллинеарный
=(0,–3,–3), примем (удобнее) за вектор нормали коллинеарный 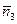 =(0,1,1). Используя точку
=(0,1,1). Используя точку  =(0,0,1) и вектор
=(0,0,1) и вектор 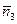 , запишем
, запишем 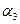 :
: 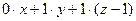 = 0, или
= 0, или 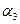 :
: 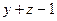 =0.
=0.
7). В этом случае имеем 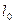 :
: 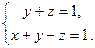 . Видим, что в задачнике плоскость
. Видим, что в задачнике плоскость 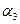 записана с погрешностью. Проверка показывает, что точка
записана с погрешностью. Проверка показывает, что точка 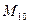 не удовлетворяет второму уравнению!
не удовлетворяет второму уравнению!
Ответ: в случае: а)  :
: 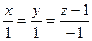 ,
,  :
: 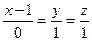 ; б)
; б) 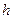 =
= 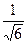 ; в)
; в) 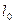 :
: 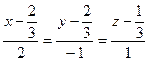 .
.
☻
Вопросы для самопроверки:
1. При помощи какого свойства векторов получают общее уравнение плоскости?
2. Как записывается уравнение плоскости, проходящей через заданную точку?
3. Что значит «уравнение плоскости в отрезках»?
4. Как получают каноническое уравнение прямой линии в пространстве?
5. Какой физический смысл имеет параметрическое задание уравнения прямой в пространстве?
6. Как получают уравнение прямой, проходящей через две заданные точки?
7. Что такое «отклонение» точки от заданной плоскости, как его вычисляют?
8. Как нормализовать общее уравнение плоскости?
9. Как определить угол между заданными прямыми линиями в пространстве?
10. Как записывают условия параллельности и перпендикулярности для двух прямых в пространстве?
11. Какие задачи в пространстве вызвали наибольший интерес (восторг!)?
Задачи для самоподготовки:
Пример C5 – 1: Составить уравнение плоскости, которая проходит через точки  и
и 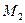 параллельно вектору
параллельно вектору  , в случае: а)
, в случае: а)  (1,2,0),
(1,2,0), 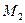 (2,1,1),
(2,1,1),  =(3,0,1); б)
=(3,0,1); б)  (1,1,1),
(1,1,1), 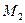 (2,3,–1),
(2,3,–1),  =(0,–1,2).
=(0,–1,2).
Ответ: в случае: а)  :
: 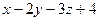 =0; б)
=0; б)  :
: 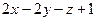 =0.
=0.
Пример C5 – 2: Заданы две плоскости  :
: 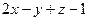 =0 и
=0 и  :
: 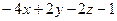 =0. Определить их взаимное расположение: пересекаются, параллельны или совпадают. Найти расстояние между плоскостями и косинус угла между ними.
=0. Определить их взаимное расположение: пересекаются, параллельны или совпадают. Найти расстояние между плоскостями и косинус угла между ними.
Ответ: плоскости параллельны, расстояние между ними:  =
=  .
.
Пример C5 – 3: Заданы две плоскости  и
и  . Написать уравнение плоскости
. Написать уравнение плоскости 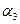 , равноудалённой от заданных плоскостей. Рассмотреть случаи:
, равноудалённой от заданных плоскостей. Рассмотреть случаи:
а)  :
: 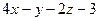 =0 и
=0 и  :
: 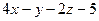 =0;
=0;
б)  :
: 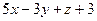 =0 и
=0 и  :
: 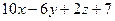 =0.
=0.
Ответ: в случаях: а) 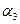 :
: 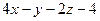 =0; б)
=0; б) 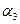 :
: 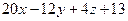 =0.
=0.
Пример C5 – 4: Определить, лежат ли точки  (2,–1,1) и
(2,–1,1) и  (1,2,–3) в одном, в смежных или вертикальных углах, образованных при пересечении двух плоскостей, Для случая: б)
(1,2,–3) в одном, в смежных или вертикальных углах, образованных при пересечении двух плоскостей, Для случая: б)  :
: 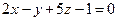 =0 и
=0 и  :
: 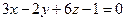 .
.
Ответ: в случае б) точки  ,
,  расположены в вертикальных углах.
расположены в вертикальных углах.
Пример C5 – 5: Составить каноническое уравнение прямой линии, проходящей через точки  и
и 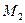 . Рассмотреть случаи: а)
. Рассмотреть случаи: а)  (1,–2,1),
(1,–2,1), 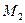 (3,1,–1); б)
(3,1,–1); б)  (3,–1,0),
(3,–1,0), 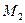 (1,0,–3).
(1,0,–3).
Ответ: в случае: а)  :
: 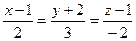 , б)
, б)  :
: 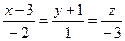 .
.
< * * * * * >
☺ ☻ ☺
Контрольная работа №1 предназначена оценить степень усвоения основных терминов, определений и свойств геометрических фигур, изучаемых «Аналитической геометрии».
Состав и степень трудности предлагаемых в Контрольной работе заданий согласовывается с Методическим советом кафедры «Высшая математика».
При разработке заданий Контрольной работы учитывается также требование побудить студентов повторить пройденный материал по предмету. Это значит, что в заданиях не должно быть ничего такого, что, так или иначе, требует самостоятельных обобщений и выводов со стороны студентов.
Перед выполнением Контрольной работы студенты должны ознакомиться с перечнем вопросов, которые будут отражены в заданиях. Так же важным элементом подготовки к контрольной работе должны быть регулярные текущие контрольные мероприятия в виде оперативных опросов: по 6-7 минут в начале каждого занятия.
Прием части-1 БДЗ. Приём БДЗ определяется двумя последовательными мероприятиями:
1). Формальный приём выполненных Заданий непосредственно в аудитории: проверка на соответствие правилам закрепления вариантов заданий за каждым студентом.
2). Контроль выполненных Заданий преподавателем: проверка правильности решения заданий и соответствия требованиям по оформлению каждого задания БДЗ.
3). Защита выполненных заданий БДЗ каждым студентом в специально назначенное время (обычно, в день консультаций по предмету). Определение окончательной оценки качества выполнения Части-1 БДЗ.
Замечание: 1). Сборник заданий по БДЗ находится в информационной системе института с самого начала семестра, постоянно.
2). Сборник заданий по БДЗ содержит по каждому заданию примеры решения и оформления.
< * * * * * >
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 526; Нарушение авторских прав?; Мы поможем в написании вашей работы!