
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 6. Контрольная работа №1. Прием части-1 БДЗ. 2 страница
|
|
|
|
8. Как можно вычислить высоту параллелепипеда, построенного на тройке векторов  ,
,  ,
,  , приведенных к общему началу?
, приведенных к общему началу?
9. Как можно определить тип тройки векторов  ,
,  ,
,  , заданных их декартовыми координатами?
, заданных их декартовыми координатами?
10. Как проверить, являются ли векторы  ,
,  ,
,  компланарными?
компланарными?
Задачи для самоподготовки:
Пример C3 – 1: Вычислить площадь треугольника с вершинами  (1,1,1),
(1,1,1),  (2,3,4),
(2,3,4),  (4,3,2).
(4,3,2).
Ответ: площадь треугольника: 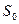 =2
=2 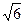 .
.
Пример C3 – 2: При каких значениях  и
и 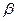 вектор
вектор 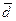 =
= 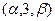 коллинеарен вектору
коллинеарен вектору  =
=  , если
, если  =(3,–1,1) и
=(3,–1,1) и  =(1,2,0).
=(1,2,0).
Ответ:значения:  =–6,
=–6, 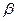 =21.
=21.
Пример C3 – 3: Силы  =(2,–1,–3),
=(2,–1,–3), 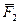 =(3,2,–1),
=(3,2,–1),  =(–4,1,3) приложены к точке
=(–4,1,3) приложены к точке  =(–1,4,2). Определить суммарный момент сил относительно точки
=(–1,4,2). Определить суммарный момент сил относительно точки 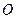 =(2,3,–1): вычислить величину и направляющие косинусы.
=(2,3,–1): вычислить величину и направляющие косинусы.
Ответ:  =7
=7 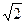 и
и 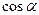 =
= 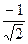 ,
, 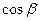 =0,
=0, 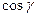 =
= 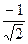 .
.
Пример C3 – 4: Заданы векторы:  =(1,–1,3),
=(1,–1,3),  =(–2,2,1),
=(–2,2,1),  =(3,–2,5). Вычислить
=(3,–2,5). Вычислить 

 . Какова ориентация троек: а)
. Какова ориентация троек: а)  ,
,  ,
,  ; б)
; б)  ,
,  ,
,  ; с)
; с)  ,
,  ,
,  .
.
Ответ: в случаях: а) левая тройка, б) и в) тройки правые.
Пример C3 – 5: Доказать, что четыре точки:  =(1,2,–1),
=(1,2,–1),  =(0,1,5),
=(0,1,5),  =(–1,2,1),
=(–1,2,1), 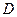 =(2,1,3) лежат в одной плоскости.
=(2,1,3) лежат в одной плоскости.
Ответ: доказано применением смешанного произведения: 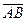
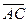
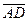 =0.
=0.
< * * * * * >
☺ ☻ ☺
Если на плоскости заданы точка 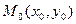 и вектор
и вектор  , перпендикулярный прямой
, перпендикулярный прямой  , то уравнение этой прямой можно записать в виде:
, то уравнение этой прямой можно записать в виде:
 :
:  = 0, (1)
= 0, (1)
уравнение (1) можно записать в виде:  , или
, или  – общее уравнение прямой линии.
– общее уравнение прямой линии.
Если уравнение  умножить на число:
умножить на число:  , причём выбирают знак
, причём выбирают знак 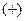 , если
, если 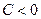 , и знак
, и знак 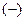 , если
, если 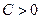 , то получают запись:
, то получают запись:  , которую называют уравнением прямой линии в нормальном виде. Нормализованное уравнение удобно применять при вычислении отклонения точки
, которую называют уравнением прямой линии в нормальном виде. Нормализованное уравнение удобно применять при вычислении отклонения точки 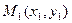 от прямой линии
от прямой линии  , определяемое выражением:
, определяемое выражением: 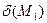 =
= 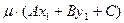 , и расстояния:
, и расстояния: 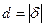 .
.
Если заданы точки:  ,
, 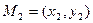 , принадлежащие
, принадлежащие  , то уравнение прямой в этом случае удобно записать в виде:
, то уравнение прямой в этом случае удобно записать в виде: 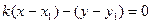 , где
, где  . В этом случае имеем:
. В этом случае имеем:  .
.
Если выбрать точки специально:  ,
, 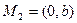 , то уравнение прямой линии можно записать в виде:
, то уравнение прямой линии можно записать в виде: 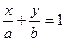 – уравнение в отрезках.
– уравнение в отрезках.
Если прямая линия  задана точкой
задана точкой  и направляющим вектором
и направляющим вектором 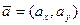 , то уравнение записывают в виде:
, то уравнение записывают в виде: 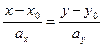 – каноническое уравнение.
– каноническое уравнение.
Учитывая, что векторы  =
= 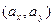 и
и 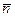 =
= 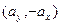 взаимно перпендикулярны, имея направляющий вектор
взаимно перпендикулярны, имея направляющий вектор  прямой
прямой  , мы можем записывать сразу:
, мы можем записывать сразу:
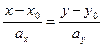 , или
, или 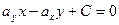 , где
, где  =
=  . (2)
. (2)
Замечание: аналогично: имея вектор  , можем сразу записать
, можем сразу записать  =
= 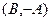 , а потом выбирать вариант записи уравнения
, а потом выбирать вариант записи уравнения  в общем виде или в канонической форме!
в общем виде или в канонической форме!
••• ≡ •••
Пример 1 – 141: Прямая линия задана точкой 
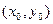 и вектором нормали
и вектором нормали 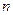 =
= 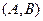 . Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи: а) точка
. Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи: а) точка  (–1,2),
(–1,2), 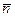 =(2,2); б)
=(2,2); б)  (2,1),
(2,1), 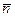 =(2,0).
=(2,0).
Решение:
Общие формулы: общее уравнение:  , где
, где  =
= 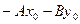 ; нормальное уравнение
; нормальное уравнение  ; расстояние от точки
; расстояние от точки 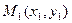 до
до  :
: 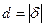 , где
, где  ; в нашем примере
; в нашем примере  .
.
1). Для случая а) имеем: общее уравнение можем записать в виде  =0, или в виде
=0, или в виде  =0; для нормализации общего уравнения вычислим
=0; для нормализации общего уравнения вычислим  =
= 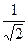 → нормальное уравнение:
→ нормальное уравнение: 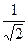 ·(
·( )=0 → отклонение
)=0 → отклонение 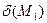 = –
= – 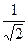 →
→ 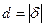 =
= 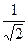 .
.
2). Для случая б) имеем: общее уравнение можем записать в виде  =0, или в виде
=0, или в виде  =0; для нормализации общего уравнения вычислим
=0; для нормализации общего уравнения вычислим  =1 → нормальное уравнение: 1·(
=1 → нормальное уравнение: 1·( )=0 → отклонение
)=0 → отклонение 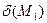 = –2→
= –2→ 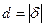 = 2.
= 2.
Ответ: в случае: а) уравнения: общее  =0, нормальное
=0, нормальное 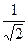 ·(
·( )=0,
)=0,  =
= 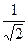 ; б) уравнения: общее
; б) уравнения: общее  =0, нормальное
=0, нормальное  =0,
=0,  =2.
=2.
Пример 2 – 142: Прямая линия задана точкой 
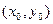 и направляющим вектором
и направляющим вектором  =
= 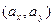 . Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи:
. Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи:
а) точка  (–1,2),
(–1,2),  =(3,–1); б)
=(3,–1); б)  (1,1),
(1,1),  =(0,–1).
=(0,–1).
Решение:
Замечание: каждую новую задачу нужно попытаться решить, максимально используя уже отработанные средства и алгоритмы!
Общие формулы: учтём, что векторы  =
= 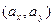 и
и 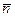 =
= 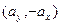 взаимно перпендикулярны; заменяем
взаимно перпендикулярны; заменяем  на
на 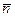 =
= 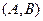 и далее применяем все выражения предыдущего Примера: общее уравнение
и далее применяем все выражения предыдущего Примера: общее уравнение  , где
, где  =
= 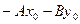 ; нормальное уравнение
; нормальное уравнение  ; расстояние от точки
; расстояние от точки 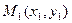 до
до  :
: 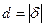 , где
, где  ; в нашем примере
; в нашем примере  .
.
1). Для случая а) имеем 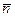 =(1,3): общее уравнение можем записать в виде
=(1,3): общее уравнение можем записать в виде 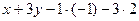 =0, или в виде
=0, или в виде 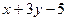 =0; для нормализации общего уравнения вычислим
=0; для нормализации общего уравнения вычислим  =
= 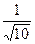 → нормальное уравнение:
→ нормальное уравнение: 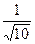 ·(
·(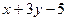 )=0 → отклонение
)=0 → отклонение 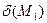 = –
= –  →
→ 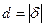 =
=  .
.
2). Для случая б) имеем 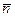 =(1,0): общее уравнение можем записать в виде
=(1,0): общее уравнение можем записать в виде  =0, или в виде
=0, или в виде 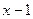 =0; для нормализации общего уравнения вычислим
=0; для нормализации общего уравнения вычислим  =1 → нормальное уравнение: 1·(
=1 → нормальное уравнение: 1·(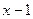 )=0 → отклонение
)=0 → отклонение 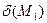 = –1→
= –1→ 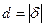 =1.
=1.
Ответ: в случае: а) уравнения: общее 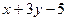 =0, нормальное
=0, нормальное 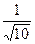 ·(
·(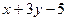 )=0,
)=0,  =
=  ; б) уравнения: общее
; б) уравнения: общее 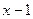 =0, нормальное
=0, нормальное 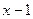 =0,
=0,  =1.
=1.
Пример 3 – 144: Задана прямая линия  и точкой
и точкой 
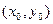 . Вычислить расстояние от точки
. Вычислить расстояние от точки  до
до  . Записать уравнение прямой
. Записать уравнение прямой  , проходящей через точку
, проходящей через точку  перпендикулярно
перпендикулярно  . Записать уравнение прямой
. Записать уравнение прямой 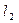 , проходящей через точку
, проходящей через точку  параллельно
параллельно  . Рассмотреть случаи: а)
. Рассмотреть случаи: а)  :
: 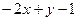 =0, точка
=0, точка  (–1,2).
(–1,2).
Решение:
Замечание: каждую новую задачу нужно попытаться решить, максимально используя уже отработанные средства и алгоритмы!
Общие формулы: имея уравнение прямой, записываем: 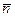 =
= 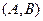 – вектор нормали и
– вектор нормали и  =
= 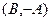 – направляющий вектор, они взаимно перпендикулярны; векторы
– направляющий вектор, они взаимно перпендикулярны; векторы 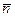 и
и  будут использованы для построения прямой, проходящей через точку
будут использованы для построения прямой, проходящей через точку  параллельно или перпендикулярно заданной прямой
параллельно или перпендикулярно заданной прямой  ; получение нормального уравнения и вычисление расстояние от точки
; получение нормального уравнения и вычисление расстояние от точки  до прямой
до прямой  выполняется также, как и в предыдущих примерах.
выполняется также, как и в предыдущих примерах.
1). Для случая а) вычисляем  =
= 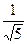 → нормальное уравнение:
→ нормальное уравнение: 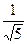 ·(
·(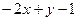 )=0 → отклонение
)=0 → отклонение  =
= 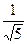 ·
·  =3→
=3→ 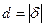 =
=  .
.
2). Первый способ. Прямая, перпендикулярная  , должна иметь общее уравнение
, должна иметь общее уравнение  :
:  =0, где коэффициент
=0, где коэффициент  вычисляется из условия
вычисляется из условия 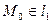 . Имеем
. Имеем  =0 →
=0 →  =–3. Окончательно
=–3. Окончательно  :
: 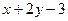 =0. Второй способ. Из уравнения прямой
=0. Второй способ. Из уравнения прямой  следует направляющий вектор прямой
следует направляющий вектор прямой  , именно:
, именно:  =
= 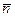 =(–2,1). После этого можем записать каноническое уравнение
=(–2,1). После этого можем записать каноническое уравнение  :
:  .
.
3). Первый способ. Прямая, параллельная  , должна иметь общее уравнение
, должна иметь общее уравнение  :
: 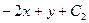 =0, где коэффициент
=0, где коэффициент 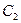 вычисляется из условия
вычисляется из условия 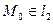 . Имеем
. Имеем  =0 →
=0 → 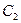 =–4. Окончательно
=–4. Окончательно  :
:  =0. Второй способ. Из уравнения прямой
=0. Второй способ. Из уравнения прямой  следует направляющий вектор прямой
следует направляющий вектор прямой  , именно:
, именно: 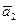 =
=  =(1,2). После этого можем записать каноническое уравнение
=(1,2). После этого можем записать каноническое уравнение  :
:  .
.
Ответ: в случае: а) расстояние от точки  :
:  =
=  , уравнения
, уравнения  :
: 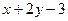 =0,
=0,  :
:  =0, или в каноническом виде
=0, или в каноническом виде  :
:  ,
,  :
:  .
.
Пример 4 – 150: Треугольник  задан координатами своих вершин. Записать уравнения прямых линий:
задан координатами своих вершин. Записать уравнения прямых линий: 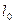 , содержащей сторону треугольника
, содержащей сторону треугольника 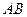 ,
, 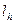 , содержащей высоту
, содержащей высоту 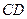 , биссектрис
, биссектрис  внутреннего и
внутреннего и 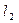 внешнего угла при вершине
внешнего угла при вершине  . Вычислить длину высоты
. Вычислить длину высоты 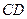 =
= 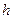 и угол
и угол 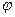 между высотой
между высотой 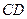 и медианой
и медианой 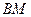 . Рассмотреть случаи: а)
. Рассмотреть случаи: а)  (1,2),
(1,2),  (2,–2),
(2,–2),  (6,1).
(6,1).
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 521; Нарушение авторских прав?; Мы поможем в написании вашей работы!