
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 6. Контрольная работа №1. Прием части-1 БДЗ. 1 страница
|
|
|
|
ЗАНЯТИЕ 5. Различные виды уравнения плоскости в пространстве: общее, неполное, в отрезках, проходящее через три точки, проходящее через точку нормально данному вектору. Расстояние от точки до плоскости. Угол между прямой и плоскостью. Канонические уравнения прямой в пространстве.
ЗАНЯТИЕ 4. Различные виды уравнения прямой на плоскости: общее, параметрическое, каноническое, через угловой коэффициент, проходящее через две точки. Определение угла между прямыми. Условия параллельности и перпендикулярности. Расстояние от точки до прямой.
ЗАНЯТИЕ 3. Правые и левые тройки векторов. Векторное произведение векторов: определение и свойства (физический смысл). Векторное произведение векторов, заданных своими проекциями. Смешанное произведение векторов.
☺ ☻ ☺
Пусть векторы  ,
,  ,
,  образуют правую тройку. Векторное произведение для векторов
образуют правую тройку. Векторное произведение для векторов  ,
,  записывают в виде:
записывают в виде:  =
=  x
x  =
=  =
=  ∙
∙ 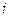 –
–  ∙ j +
∙ j +  ∙ k =
∙ k = 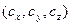 , причём
, причём 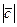 =
=  =
= 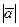 ∙
∙ 
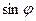 , где
, где 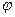 – угол между векторами
– угол между векторами  ,
,  (известно:
(известно:  , то есть
, то есть 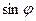 ≥0).
≥0).
Для векторов  ,
,  ,
,  определено векторно-скалярное, то есть смешанное, произведение: (
определено векторно-скалярное, то есть смешанное, произведение: ( x
x  )∙
)∙  или
или  ∙(
∙( x
x  ). В координатной форме вычисление определяется выражением:
). В координатной форме вычисление определяется выражением:
( x
x  )∙
)∙  =
= 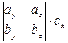 –
–  +
+ 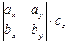 =
=  =
= 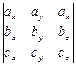 =
= 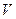 .
.
Известно, что векторное произведение обладает свойствами: 1)  =
= 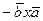 , 2)
, 2) 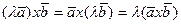 , 3)
, 3) 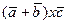 =
= 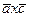 +
+  .
.
Используют также выражение: |( x
x  )∙
)∙  |=|
|=|  |∙|
|∙|  |∙|
|∙|  |∙
|∙ 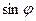 ∙
∙ 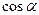 =| V | – объём параллелепипеда, построенного на векторах
=| V | – объём параллелепипеда, построенного на векторах  ,
,  ,
,  . Из последнего следует условие компланарности этих векторов: (
. Из последнего следует условие компланарности этих векторов: ( x
x  )∙
)∙  =0.
=0.
••• ≡ •••
Пример 1 – 98: Векторы  и
и  образуют угол
образуют угол 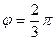 . Зная, что
. Зная, что 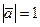 ,
, 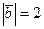 , вычислить: 1)
, вычислить: 1) 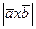 , 2)
, 2) 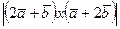 , 3)
, 3) 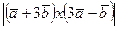 .
.
Замечание: применение вместо записи векторов в виде:  и
и  предпочтительнее, чем использование записей векторов с индексами (учитывая почерк большинства!).
предпочтительнее, чем использование записей векторов с индексами (учитывая почерк большинства!).
Решение:
Применяя общие формулы, решим каждую из поставленных задач:
1). Вычислим: 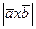 =
= 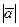 ∙
∙ 
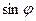 =
=  =
= 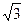 .
.
2). Преобразуем выражение: 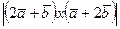 =
= 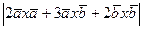 =3
=3 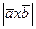 =3
=3 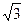 .
.
3). Как в пункте 2): 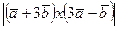 =
=  =10
=10 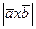 =10
=10 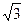 .
.
Ответ: 1) 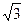 , 2) 3
, 2) 3 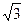 , 3) 10
, 3) 10 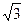 .
.
Пример 2 – 106: Даны векторы  = (3, – 1,2),
= (3, – 1,2),  = (1,2, – 1). Найти координаты векторных произведений: 1)
= (1,2, – 1). Найти координаты векторных произведений: 1)  , 2)
, 2)  , 3)
, 3) 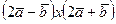 .
.
Решение:
Применяя общие формулы, решим каждую из поставленных задач:
1).Воспользуемся формулой: 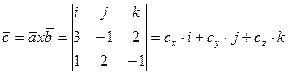 , где:
, где:
 ,
, 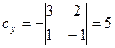 ,
,  →
→  .
.
2). С учетом результата п. 1: 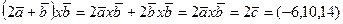 .
.
3). С учетом п. 1: 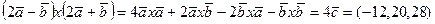 .
.
Замечание: преобразования в п. 1), 2), 3) учитывают свойства векторного произведения.
Ответ: 1): (–3,5,7); 2): (–6,10,14); 3): (–12,20,28).
Пример 3 – 115: Сила 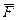 =(2,–4,5) приложена к точке
=(2,–4,5) приложена к точке  =(4,–2,3). Определить момент этой силы относительно точки
=(4,–2,3). Определить момент этой силы относительно точки 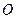 =(3,2,–1).
=(3,2,–1).
Решение:
 Общие формулы: в физике моментом силы относительно неподвижной точки называют вектор, вычисляемый по формуле:
Общие формулы: в физике моментом силы относительно неподвижной точки называют вектор, вычисляемый по формуле: 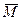 =
= 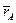 x
x 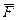 =
=  , где
, где 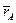 – радиус-вектор из точки
– радиус-вектор из точки 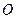 в точку
в точку  приложения силы
приложения силы 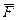 (на самом деле, вместо точки приложения силы
(на самом деле, вместо точки приложения силы 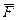 , может быть использована любая точка, принадлежащая линии действия этой силы).
, может быть использована любая точка, принадлежащая линии действия этой силы).
Применяя общую формулу, запишем решение поставленной задачи:
1). Вычислим радиус-вектор: 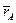 =
= 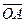 =
=  =(4,–2,3) –(3,2,–1)= (1,–4,4).
=(4,–2,3) –(3,2,–1)= (1,–4,4).
2). Вычислим вектор момента силы 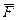 относительно неподвижной точки
относительно неподвижной точки 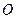 :
: 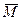 =
= 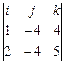 =
= 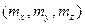 , где:
, где: 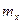 =
=  =–4,
=–4, 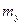 =–
=–  =–3,
=–3, 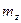 =
= 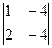 =4 →
=4 → 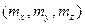 =(–4,3,4).
=(–4,3,4).
Ответ: моментом силы: 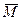 =(–4,3,4).
=(–4,3,4).
Пример 4 – 127: Установить, образуют ли векторы:  ,
,  ,
,  базис в множестве векторов пространства
базис в множестве векторов пространства  : 1)
: 1)  = (2,3,–1),
= (2,3,–1),  = (1, – 1,3),
= (1, – 1,3),  = (1,9,–11),
= (1,9,–11),
2)  = (3,–2,1),
= (3,–2,1),  = (2,1,2),
= (2,1,2),  = (3,–1,–2).
= (3,–1,–2).
Решение:
Общие формулы: известно, что векторы  ,
,  ,
,  образуют базис, то есть независимы, если они не принадлежат одной плоскости или параллельным плоскостям; для проверки этого условия используют определитель
образуют базис, то есть независимы, если они не принадлежат одной плоскости или параллельным плоскостям; для проверки этого условия используют определитель 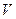 =
= 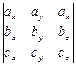 : если
: если 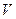
 0, то векторы независимы, если
0, то векторы независимы, если 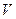 =0, то зависимы.
=0, то зависимы.
Применяя названный критерий, решим каждую из поставленных задач:
1). Вычислим определитель: 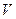 =
=  =2
=2  –1
–1 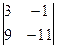 +1
+1 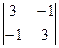 =0. Следует: векторы не образуют базис.
=0. Следует: векторы не образуют базис.
2). Вычислим определитель: 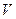 =
=  =3
=3  –2
–2 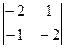 +3
+3 
 0. Следует: векторы образуют базис.
0. Следует: векторы образуют базис.
Ответ: для случаев: а) не образуют, б) образуют.
Пример 5 – 132: Вычислить объём тетраэдра  , если
, если 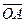 =
=  ,
, 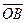 =
=  ,
,  =
= 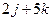 .
.
 Решение:
Решение:
Замечание: задачу можно было решать без рисунка (достоинство аналитической геометрии), но мы воспользуемся простым эскизом для побуждения зрительного образа решения задачи.
Алгоритм:
1) вспомним: объём пирамиды равен 1/3 объёма соответствующей призмы;
2) обозначим объём пирамиды – 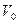 , а объём параллелепипеда, построенного на векторах
, а объём параллелепипеда, построенного на векторах  =
= 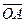 ,
,  =
= 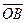 ,
,  =
=  –
– 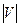 ; вычислим
; вычислим 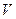 =
= 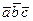 – величина объёма со знаком;
– величина объёма со знаком;
3) учтём, что 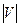 =6
=6 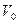 и запишем результат
и запишем результат 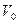 =
= 
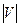 .
.
Реализуем принятый алгоритм:
1). Вычислим смешанное произведение векторов  ,
,  ,
,  :
:
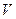 =
= 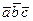 =
= 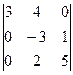 =3
=3  +0 +0 =–51.
+0 +0 =–51.
2). Вычислим объём пирамиды: 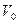 =
= 
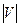 =
=  .
.
Ответ: объём пирамиды: 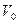 =
= 
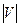 =
=  .
.
•◄ Дополнительно ►•
Пример 6 – 100: Упростить выражения: 1)  =
= 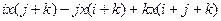 ,
,
2)  =
= 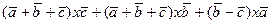 ,
,
3)  =
= 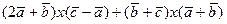 ,
,
4) 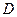 =
=  ,
,
Решение:
Воспользуемся таблицей векторного умножения единичных ортогональных векторов 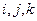 :
:

| 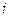 x i =0 x i =0
|  x x 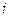 = – = – 
|  x x 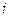 = = 
|
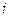 x x  = k = k
|  x x  =0 =0
|  x x  = –i = –i
| |
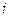 x x  = – = – 
|  x x  = = 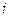
|  x x  =0 =0
|
Замечание: использование цикла подсказывает результат: если в левой части пара букв названа в направлении движения по стрелке, то в правой части называем третью букву со знаком плюс, если пара букв названа против направления стрелки, то в правой части появляется знак минус.
1). Используя таблицу умножения, запишем:  =
=  =
=  .
.
2). Упростим:  =
= 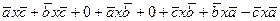 =
= 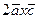 .
.
3). Упростим:  =
=  =
=  .
.
4). Используя таблицу умножения, запишем: 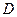 =
= 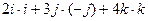 =3.
=3.
Ответ: выражения: 1)  , 2)
, 2) 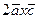 , 3)
, 3)  , 4) 3.
, 4) 3.
Пример 7 – 103: Векторы  ,
,  и
и  удовлетворяют условию:
удовлетворяют условию: 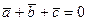 . Доказать, что верны равенства:
. Доказать, что верны равенства:  .
.
Решение:
Аналитический способ:
1). Докажем, что:  – доказано!
– доказано!
2). Докажем, что: 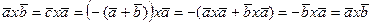 – доказано!
– доказано!
Замечание: преобразования в пунктах 1) и 2) учитывают свойства векторного произведения.
Геометрический способ:
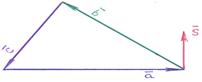
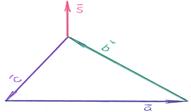
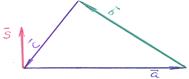
1). Векторное равенство: 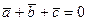 означает, что последовательная цепочка векторов
означает, что последовательная цепочка векторов  ,
,  ,
,  замыкается в виде треугольника!
замыкается в виде треугольника!
| 
| 
|
2). Это значит, что 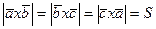 – удвоенная площадь треугольника, образованного векторами
– удвоенная площадь треугольника, образованного векторами  ,
,  ,
,  . На рисунках последовательно представлены векторные произведения:
. На рисунках последовательно представлены векторные произведения:  ,
,  ,
, 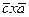 .
.
3). Так как в выражениях  векторы
векторы  ,
,  ,
,  применяются в соответствии с циклической перестановкой:
применяются в соответствии с циклической перестановкой:  , то
, то 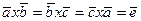 , что завершает доказательство, так как теперь имеем
, что завершает доказательство, так как теперь имеем 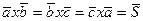 !
!
Замечание: одновременное применение аналитического и геометрического способов делает задачу особенно привлекательной!
Ответ: доказательство представлено в тексте!
☻
Вопросы для самопроверки:
1. Что значит «тройка векторов  ,
,  ,
,  »?
»?
2. Какие свойства векторного произведения относят к геометрическим свойствам?
3. Какие свойства векторного произведения относят к алгебраическим свойствам?
4. Какой физический смысл векторного произведения (в механике)?
5. Как при помощи векторного произведения проверить, являются ли векторы  ,
,  коллинеарными?
коллинеарными?
6. Как можно вычислить площадь «пространственного треугольника»?
7. Что такое векторно-скалярное (скалярно-векторное) произведение векторов  ,
,  ,
,  ?
?
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 514; Нарушение авторских прав?; Мы поможем в написании вашей работы!