
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 2. Определители 2-го порядка и системы линейных уравнений с двумя неизвестными. Определители 3-го порядка. Простейшие правила вычисления определителей. 2 страница
|
|
|
|
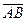 =
= 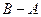 =(1,–5,7)–(–3,5,6)=(4,–10,1),
=(1,–5,7)–(–3,5,6)=(4,–10,1), 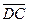 =
=  =(8,–3,–1)–(4,7,–2)=(4,–10,1),
=(8,–3,–1)–(4,7,–2)=(4,–10,1),
подтверждено: 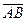 =
= 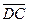 .
.
2). Вычислим вектор 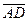 :
:
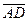 =
=  =(4,7,–2)–(–3,5,6)=(7,2,–8). Вычислим:
=(4,7,–2)–(–3,5,6)=(7,2,–8). Вычислим: 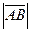 =
=  и
и  =
=  , подтверждено:
, подтверждено: 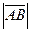 =
= 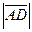 .
.
3). Вычислим векторы 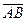 ·
· 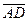 =(4,–10,1)·(7,2,–8)=
=(4,–10,1)·(7,2,–8)=  =0:
=0: 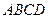 – ромб.
– ромб.
Замечание: возможны и другие варианты решения задачи!
Ответ: показан алгоритм доказательства и его реализация: доказано.
Пример 8 – 84: Вычислить работу силы  =
= 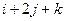 при перемещении материальной точки из положения
при перемещении материальной точки из положения  (–1,2,0) в положение
(–1,2,0) в положение  =(2,1,3).
=(2,1,3).
Решение:
Замечание: в условии задачи следует добавить: перемещение из положения  в положение
в положение  происходит по прямой линии!
происходит по прямой линии!
1). Вычислим перемещение  =
= 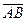 =
= 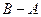 =(2,1,3)– (–1,2,0)=(3,–1,3).
=(2,1,3)– (–1,2,0)=(3,–1,3).
2). Вычислим работу силы: 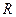 =|
=| 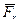 |·|
|·|  | =
| =  ·
·  =(1,2,1)·(3,–1,3)=
=(1,2,1)·(3,–1,3)=  =4.
=4.
Ответ: работа: 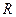 =4.
=4.
•◄ Дополнительно ►•
Пример 9 – 48: Заданы векторы:  =(1,5,3),
=(1,5,3),  =(6,–4,–2),
=(6,–4,–2),  =(0,–5,7),
=(0,–5,7), 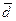 =(–20,27,–35). Требуется подобрать числа
=(–20,27,–35). Требуется подобрать числа  так, чтобы образовалась замкнутая ломаная линия, составленная из векторов:
так, чтобы образовалась замкнутая ломаная линия, составленная из векторов:  ,
,  ,
,  и
и 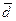 .
.
Решение:
Замечание: если рассеять туман из условия задачи, то имеется в виду что за счёт коэффициентов  необходимо обеспечить:
необходимо обеспечить:  +
+  +
+  +
+ 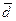 =0.
=0.
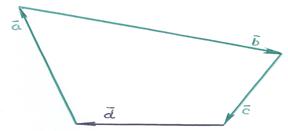 1). Рисунок отражает ситуацию, для которой:
1). Рисунок отражает ситуацию, для которой:  =1. Далее запускаем процесс:
=1. Далее запускаем процесс:
 →
→  ,
,  →
→  ,
,  →
→  .
.
2). Запишем равенство  +
+  +
+  +
+ 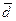 =0 в координатной форме:
=0 в координатной форме:
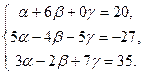
3). Решая систему уравнений методом Гаусса, получаем:  ,
,  ,
, 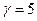 .
.
Ответ: числа:  ,
,  ,
, 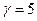 .
.
Пример 10 – 77: Зная, что  =3,
=3, 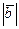 =1,
=1, 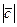 =4 и имея равенство:
=4 и имея равенство:  +
+  +
+  =0, вычислить сумму:
=0, вычислить сумму:  ·
·  +
+  ·
·  +
+  ·
·  .
.
Замечание: задачу можно отнести к этюду-шутке!
Решение:
1). Запишем сумму: 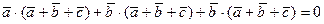 . Применяя свойства скалярного произведения, получим:
. Применяя свойства скалярного произведения, получим:  .
.
2). Учтём:  =
=  =9,
=9, 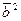 =
=  =1,
=1, 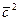 =
=  =16. Тогда:
=16. Тогда:  ·
·  +
+  ·
·  +
+  ·
·  =–13.
=–13.
Ответ: значение суммы:  ·
·  +
+  ·
·  +
+  ·
·  =–13.
=–13.
☻
Вопросы для самопроверки:
1. При помощи какого свойства векторов получают общее уравнение прямой?
2. Как записываются уравнения прямой линии в параметрической форме?
3. Что значит «уравнение прямой линии в отрезках»?
4. Как проводится «нормализация общего уравнения прямой линии»?
5. Что значит «угловой коэффициент» вектора, прямой?
6. Как получают уравнение прямой, проходящей через две заданные точки?
7. Что такое «отклонение» точки от заданной прямой, как его вычисляют?
8. Как определить, лежат ли заданные точки  и
и  в одной полуплоскости или в разных?
в одной полуплоскости или в разных?
9. Как определить угол между заданными прямыми линиями?
10. Как записывают условия параллельности и перпендикулярности для двух прямых?
11. Как определить внутренний угол заданного треугольника?
Задачи для самоподготовки:
Пример C1 – 1: Найти длину и направляющие косинусы вектора 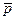 =
= 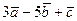 , если имеем
, если имеем  =
= 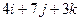 ,
,  =
= 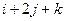 ,
,  =
=  .
.
Ответ:длина вектора  =
= 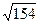 ; направляющие косинусы вектора:
; направляющие косинусы вектора: 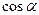 =
=  ,
, 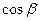 =
=  ,
, 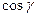 =
=  .
.
Пример C1 – 2: При каких значениях величин  и
и 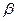 векторы
векторы  =
=  и
и  =
=  коллинеарны.
коллинеарны.
Ответ:значения:  = – 1,
= – 1, 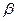 = – 4.
= – 4.
Пример C1 – 3: Даны вершины треугольника  :
:  (3,–1,5),
(3,–1,5),  (4,2,–5),
(4,2,–5),  (–4,0,3). Найти длину медианы, проведённой из вершины
(–4,0,3). Найти длину медианы, проведённой из вершины  .
.
Ответ:длина медианы:  = 7.
= 7.
Пример C1 – 4: Даны вершины треугольника  :
:  (1,–1,–3),
(1,–1,–3),  (2,1,–2),
(2,1,–2),  (–5,2,–6). Найти длину биссектрисы его внутреннего угла при вершине
(–5,2,–6). Найти длину биссектрисы его внутреннего угла при вершине  .
.
Ответ:длина биссектрисы:  =
= 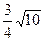 .
.
Пример C1 – 5: Треугольник задан координатами своих вершин:  (3,–2,1),
(3,–2,1),  (3,1,5),
(3,1,5),  (4,0,3). Вычислить расстояние от начала координат до точки пересечения медиан этого треугольника.
(4,0,3). Вычислить расстояние от начала координат до точки пересечения медиан этого треугольника.
Ответ:расстояние:  =
=  .
.
Пример C1 – 6: Заданы векторы:  =3,
=3, 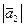 =4, угол
=4, угол 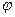 между векторами
между векторами  и
и 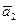 равен
равен  . Вычислить: а) скалярное произведение векторов
. Вычислить: а) скалярное произведение векторов 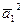 =
= 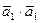 ; б)
; б)  ; в)
; в)  .
.
Ответ: по пунктам: а) 9, б) –61, в) 13.
Пример C1 – 7: Заданы векторы: 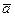 =(4,–2,–4),
=(4,–2,–4),  =(6,–3,2). Необходимо вычислить: а)
=(6,–3,2). Необходимо вычислить: а)  ; б)
; б) 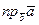 ; в) направляющие косинусы вектора
; в) направляющие косинусы вектора 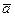 ; г)
; г) 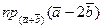 и
и 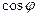 , где
, где 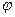 – угол между векторами
– угол между векторами  и
и  .
.
Ответ: по пунктам: а) 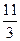 , б)
, б)  , в)
, в) 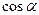 =
= 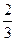 ,
, 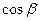 =
= 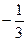 ,
, 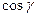 =
=  , г)
, г) 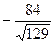 и
и 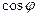 =
=  .
.
Пример C1 – 7: Найти длины сторон и величины углов треугольника с вершинами:  (–1,–2,4),
(–1,–2,4),  =(–4,–2,0),
=(–4,–2,0),  =(3,–2,1).
=(3,–2,1).
Ответ: стороны:  =
= 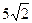 ,
,  =5,
=5, 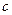 =5; углы:
=5; углы:  =
=  ,
,  =
= 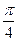 .
.
< * * * * * >
☺ ☻ ☺
Определители 2-го и 3-го порядков появились в связи с решением систем линейных уравнений 2-го и 3-го порядков. Этот факт мы будем наблюдать при изучении определителей произвольного порядка. В настоящем параграфе рассматриваются только формальные правила вычисления определителей 2-го и 3-го порядков: этого будет достаточно при изучении векторного произведения двух векторов, а также в некоторых геометрических задачах на плоскости и в пространстве.
Определители 2-го порядка.
Определителем 2-го порядка называют число, представленное в виде специальной записи:  =
= 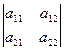 =
=  . (1)
. (1)
Говорят, что правая часть выражения (1) определяет правило вычисления определителя 2-го порядка. При использовании определителя применяют термины:
▫ элементы определителя – числа a 11, a 12, a 21, a 22;
▫ строки определителя: 1-я строка: пара чисел: a 11, a 12, 2-я строка: пара чисел a 21, a 22;
▫ столбцы определителя: 1-й столбец: пара чисел: a 11, a 21, 2-й столбец: пара чисел a 12, a 22;
▫ члены определителя: (a 11· a 22) и (– a 21· a 12).
При внимательном рассмотрении соответствия (1) нетрудно заметить правило использования элементов определителя для записи суммы левой части выражения (1). Для записи положительного члена определителя (a 11· a 22) используют схему:

Для записи отрицательного члена определителя (– a 21· a 12) используют схему:

Рассмотрим несколько примеров вычисления определителей 2-го порядка, использующих в качестве своих элементов числа, или некоторые аналитические выражения.
Пример 2 – 1: Вычислить определитель 2-го порядка:  =
= 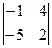 .
.
Решение:
1). Воспользуемся общей формулой:  =
= 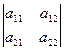 =
=  .
.
2). В нашем примере: d =(-1)·2–(-5)·4 = 18.
Ответ:  =18.
=18.
Пример 2 – 6: Вычислить определитель 2-го порядка:  =
=  .
.
Решение:
1). Воспользуемся общей формулой:  =
= 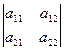 =
=  .
.
2). Прежде, чем вычислять определитель, воспользуемся формулами тригонометрии:
 =
= 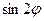 ,
, 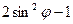 =
=  ,
, 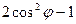 =
=  .
.
2). Перепишем определитель с учётом записанных формул:  =
=  , после чего очевиден ответ:
, после чего очевиден ответ:  =1.
=1.
Ответ:  =1.
=1.
Пример 3–8: Решить уравнение:  =
= 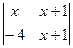 .
.
Решение:
1). Воспользуемся общей формулой вычисления:  =
= 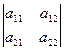 =
=  .
.
2). Вынося общий множитель второго столбца за знак определителя, получим:  =
= 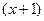
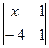 =
= 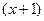 ·
· 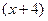 .
.
3). Из условия:  =0 получаем корни уравнения
=0 получаем корни уравнения  =–1,
=–1, 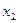 =–4.
=–4.
Ответ: корни уравнения  =–1,
=–1, 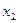 =–4.
=–4.
Замечание: формальное применение правила вычисления определителей 2-го порядка не вызывает никаких затруднений!
Определители 3-го порядка.
Определителем 3-го порядка называют число, представленное в виде специальной записи:
 =
=  =
=  +
+ 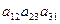 +
+  –
–  –
–  –
–  . (2)
. (2)
Говорят, что правая часть выражения (2) определяет правило вычисления определителя 3-го порядка. Соответствие, представленное выражением (2), легко запоминается, если использовать геометрическую схему составления членов определителя:


Замечание: нетрудно заметить, что правило (1) вычисления определителя 2-го порядка запомнить значительно проще, чем правило (2) для определителей 3-го порядка!
Оказывается, есть правило сведения вычисления определителя 3-го порядка к вычислению нескольких определителей 2-го порядка, а именно:
 =
=  =
=  –
–  +
+  , (3)
, (3)
или  =
=  =
=  –
–  +
+ 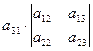 , (4)
, (4)
Обоснование правил (3) и (4) вычисления определителя 3-го порядка мы получим в теории определителей 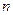 - го порядка.
- го порядка.
Замечание: правило (3) называют: вычисление определителя разложением по первой строке, а правило (4): разложение по первому столбцу.
Рассмотрим несколько примеров вычисления определителей 3-го порядка, использующих в качестве своих элементов числа, или некоторые аналитические выражения.
Пример 4 – 12: Вычислить определитель 3-го порядка:  =
= 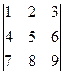 .
.
Решение:
Вычислим определитель, применяя правило (2) и учитывая принятые обозначения:  =
= 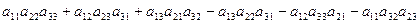 ,
,
или:  =
=  =0.
=0.
Ответ: d = 0.
Пример 5 – 15: Вычислить определитель 3-го порядка:  =
=  .
.
Решение:
1). Воспользуемся формулой (3) вычисления:
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 734; Нарушение авторских прав?; Мы поможем в написании вашей работы!