
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 7. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Общие свойства кривых второго порядка. 1 страница
|
|
|
|
☺ ☻ ☺
Окружность: основные определения и формулы:
Если точка 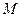
 – произвольная точка плоскости, а точка
– произвольная точка плоскости, а точка 
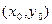 – фиксированная точка, то
– фиксированная точка, то 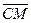 =
= 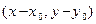 – векторная форма записи окружности, в координатной форме уравнение окружности имеет вид:
– векторная форма записи окружности, в координатной форме уравнение окружности имеет вид:
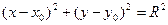 → нормальное уравнение. (1)
→ нормальное уравнение. (1)
Если центр окружности находится в начале координат  (0,0), то уравнение (1) принимает простейший вид:
(0,0), то уравнение (1) принимает простейший вид: 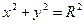 → каноническое уравнение. (2)
→ каноническое уравнение. (2)
Если вместо выражения (1) имеем равенство: 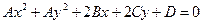 , то нетрудно получить выражение:
, то нетрудно получить выражение: 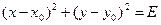 . (3)
. (3)
В зависимости от величины Е могут реализоваться такие случаи:
1). 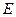 > 0, то есть
> 0, то есть 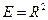 → окружность:
→ окружность: 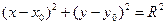 .
.
2). 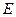 = 0 →
= 0 → 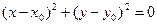 , выполняется для одной точки (x0,y0).
, выполняется для одной точки (x0,y0).
3). 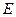 < 0, то есть →
< 0, то есть → 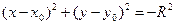 – мнимая окружность.
– мнимая окружность.
••• ≡ •••
Пример 1 – 242: Пусть  – центр окружности,
– центр окружности, 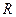 – радиус окружности,
– радиус окружности, 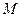 ,
,  ,
, 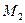 ,
, 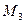 – точки окружности. Составить уравнение окружности в каждом из следующих случаев:
– точки окружности. Составить уравнение окружности в каждом из следующих случаев:
1)  (2,–3),
(2,–3), 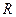 =7; 2)
=7; 2) 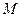 (2,6),
(2,6),  (–1,2); 3)
(–1,2); 3)  (3,2),
(3,2), 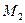 (–1,6) – концы диаметра окружности; 4)
(–1,6) – концы диаметра окружности; 4)  (1,–1), прямая линия
(1,–1), прямая линия  :
:  =0 касается окружности; 5)
=0 касается окружности; 5) 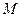 (1,2) – точка окружности, окружность касается координатных осей; 6)
(1,2) – точка окружности, окружность касается координатных осей; 6)  (3,1),
(3,1), 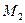 (–1,3) – точки окружности,
(–1,3) – точки окружности,  принадлежит прямой
принадлежит прямой  :
: 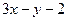 =0; 7)
=0; 7)  (–1,3),
(–1,3), 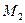 (0,2),
(0,2), 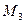 (1,–1) – точки окружности.
(1,–1) – точки окружности.
Решение:
1). Сразу записываем уравнение окружности: 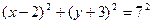 .
.
2). Из условия имеем: 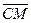 =
= 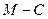 =(2,6)–(–1,2)=(3,4) →
=(2,6)–(–1,2)=(3,4) → 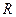 =
= 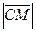 =5. Тогда уравнение окружности:
=5. Тогда уравнение окружности: 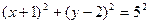 .
.
3). Так как центр окружности делит заданный отрезок пополам, то 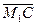 =
= 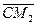 , откуда: 2
, откуда: 2  =
=  +
+ 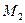 =(2,8) →
=(2,8) →  =(1,4). В то же время
=(1,4). В то же время  =
= 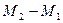 =(–4,–4) →
=(–4,–4) → 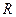 =2
=2 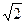 . Тогда уравнение окружности:
. Тогда уравнение окружности: 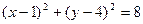 .
.
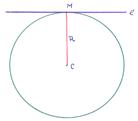 4). Радиус окружности равен расстоянию до касательной. Нормируем уравнение прямой линии и находим отклонение точки от этой прямой:
4). Радиус окружности равен расстоянию до касательной. Нормируем уравнение прямой линии и находим отклонение точки от этой прямой: 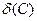 =
= 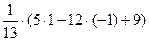 =2 →
=2 → 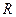 =2. Тогда
=2. Тогда  – уравнение окружности.
– уравнение окружности.
5). Обозначим радиус окружности 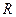 =
=  . Учитывая свойство касания окружности осей координат, запишем уравнение окружности:
. Учитывая свойство касания окружности осей координат, запишем уравнение окружности: 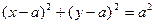 . Так как точка
. Так как точка 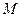 принадлежит окружности, то необходимо:
принадлежит окружности, то необходимо: 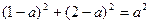 . Из уравнения получаем два корня:
. Из уравнения получаем два корня:  =1 и
=1 и  =5. Решение:
=5. Решение: 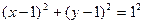 или
или 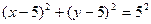 .
.
6). Точки  (3,1) и
(3,1) и 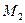 (–1,3) выделяют на окружности хорду
(–1,3) выделяют на окружности хорду 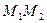 . Известна теорема, что прямая линия
. Известна теорема, что прямая линия  , проходящая через середину хорды окружности и ей перпендикулярная, проходит через центр этой окружности.
, проходящая через середину хорды окружности и ей перпендикулярная, проходит через центр этой окружности.
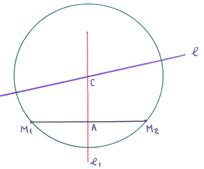 Найдём уравнение
Найдём уравнение  . Из равенства 2
. Из равенства 2  =
= 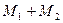 находим
находим  (1,2). Запишем
(1,2). Запишем 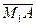 =(–2,1)=
=(–2,1)= 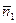 . Тогда уравнение
. Тогда уравнение  :
:  , или
, или 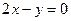 .
.
Точку пересечения прямых линий  и
и  найдём из системы уравнений:
найдём из системы уравнений: 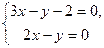 находим координаты центра
находим координаты центра  (2,4). Радиус окружности:
(2,4). Радиус окружности: 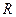 =
=  =
= 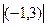 =
= 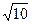 . Тогда:
. Тогда: 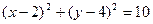 – уравнение искомой окружности.
– уравнение искомой окружности.
 7). Найдём уравнение
7). Найдём уравнение  . Из равенства 2
. Из равенства 2  =
= 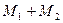 находим
находим 
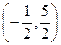 . Запишем
. Запишем 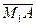 =
= 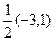 , примем
, примем 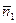 =(3,–1). Тогда уравнение
=(3,–1). Тогда уравнение  :
: 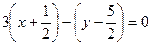 , или
, или 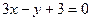 .
.
Найдём уравнение  . Из равенства векторов
. Из равенства векторов 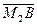 =
= 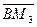 имеем 2
имеем 2  =
= 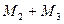 , находим
, находим 
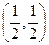 . Запишем
. Запишем 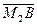 =
= 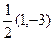 , примем
, примем 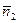 =(1,–3). Тогда уравнение
=(1,–3). Тогда уравнение  :
:  , или
, или 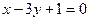 .
.
Точку пересечения прямых линий  и
и  найдём из системы уравнений:
найдём из системы уравнений: 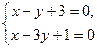 →
→  (–4,–1). Радиус окружности:
(–4,–1). Радиус окружности: 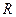 =
= 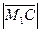 =
= 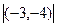 =5. Тогда:
=5. Тогда: 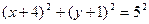 – уравнение искомой окружности.
– уравнение искомой окружности.
Ответ: 1) 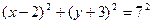 , 2)
, 2) 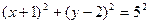 , 3)
, 3) 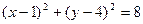 ,
,
4)  , 5)
, 5) 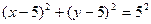 , 6)
, 6) 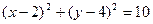 ,
,
7) 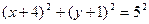 .
.
☺ ☻ ☺
Эллипс: геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Если принять, что  – большая полуось, то фокусы эллипса располагаются на оси
– большая полуось, то фокусы эллипса располагаются на оси 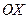 , причём:
, причём: 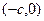 =
= 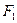 – левый фокус,
– левый фокус, 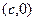 =
= 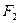 – правый фокус.
– правый фокус.
Каноническое уравнение эллипса имеет вид: 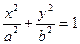 ,
,  – большая полуось,
– большая полуось,  – малая полуось. Величины
– малая полуось. Величины  ,
,  ,
, 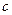 связаны соотношением:
связаны соотношением: 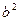 =
= 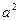 –
– 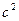 .
.
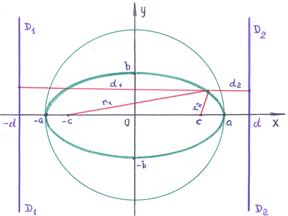 Важной характеристикой эллипса является величина:
Важной характеристикой эллипса является величина: 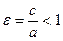 – эксцентриситет, которая определяет степень сжатия окружности вдоль оси
– эксцентриситет, которая определяет степень сжатия окружности вдоль оси 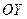 .
.
Для вычисления расстояний до фокусов используют выражения: 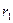 =
= 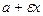 ,
, 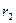 =
= 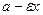 , причём
, причём 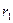 +
+ 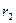 =2
=2  .
.
Особое место в свойствах эллипса занимают прямые линии: 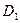 и
и 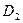 – директрисы. Положение директрис определяет число:
– директрисы. Положение директрис определяет число: 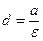 .
.
••• ≡ •••
Пример 2 – 246: Задано уравнение линии второго порядка: 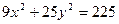 . Показать, что линия есть эллипс, записать его каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис.
. Показать, что линия есть эллипс, записать его каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис.
Решение:
1). Перепишем уравнение: 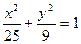 – это каноническое уравнение эллипса с фокусами, расположенными на оси
– это каноническое уравнение эллипса с фокусами, расположенными на оси  .
.
2). Полуоси эллипса:  =5,
=5,  =3. Вычислим:
=3. Вычислим:  =
= 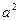 –
– 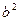 =16. Это значит:
=16. Это значит: 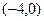 =
= 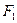 – левый фокус,
– левый фокус, 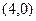 =
= 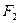 – правый фокус. Вычислим эксцентриситет:
– правый фокус. Вычислим эксцентриситет: 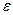 =
= 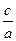 =
= 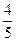 . Вычислим параметр директрисы:
. Вычислим параметр директрисы:  =
= 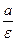 =
= 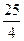 . Уравнения директрис
. Уравнения директрис 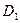 :
:  =–
=– 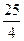 ,
,  :
:  =
= 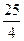 .
.
Ответ: а) уравнение эллипса 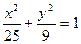 ,
,  =5,
=5,  =3; б) фокусы
=3; б) фокусы 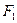 =
= 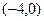 ,
, 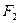 =
= 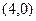 ; в) эксцентриситет
; в) эксцентриситет 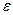 =
= 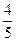 ; г) директрисы
; г) директрисы 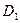 :
:  =–
=– 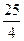 ,
, 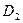 :
:  =
= 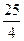 .
.
Пример 3 – 252: Главные оси эллипса совпадают с осями координат. Точки 
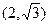 и
и 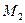 (0,2) принадлежат эллипсу. Написать уравнение эллипса, найти фокальные радиусы точки
(0,2) принадлежат эллипсу. Написать уравнение эллипса, найти фокальные радиусы точки  и расстояние этой точки до директрис.
и расстояние этой точки до директрис.
Решение:
1). Воспользуемся уравнением: 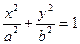 . Обозначив (для удобства!):
. Обозначив (для удобства!):  =
= 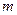 и
и 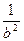 =
=  , для точек
, для точек  и
и 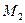 запишем систему:
запишем систему: 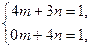 откуда
откуда 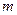 =
= 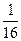 и
и 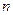 =
= 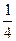 . Можем записать уравнение эллипса:
. Можем записать уравнение эллипса: 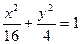 . Причём,
. Причём, 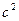 =
= 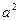 –
– 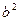 =12 и тогда запишем
=12 и тогда запишем 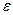 =
= 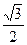 .
.
2). Вычислим фокальные радиусы для точки  , принадлежащей эллипсу: именно
, принадлежащей эллипсу: именно 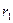 =
= 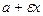 =
= 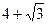 .
. 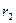 =
= 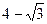 .
.
3). По определению директрисы, расстояние точки  до левой директрисы вычисляем как
до левой директрисы вычисляем как 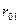 =
= 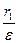 =
= 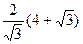 , а до правой как
, а до правой как 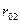 =
=  =
=  .
.
Ответ: уравнение эллипса 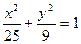 , фокальные радиусы
, фокальные радиусы 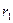 =
= 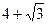 ,
, 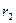 =
= 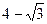 ; расстояния до директрисы
; расстояния до директрисы 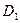 :
: 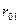 =
= 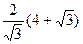 , до директрисы
, до директрисы 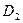 :
: 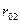 =
=  .
.
Пример 4 – 254: Написать уравнение кривой, по которой движется точка 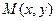 , если сумма расстояний от неё до точек
, если сумма расстояний от неё до точек 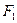 (–1,–1) и
(–1,–1) и 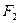 (1,1) остаётся постоянной и равна
(1,1) остаётся постоянной и равна 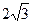 .
.
Решение:
1). Расстояние от точки 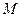 до точки
до точки 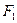 определяется выражением:
определяется выражением: 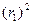 =
= 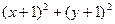 , а до точки
, а до точки 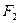 выражением:
выражением: 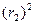 =
= 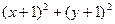 . По условию
. По условию 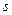 :
: 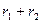 =
= 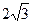 .
.
2). Выполнив тождественные преобразования выражения 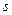 , окончательно запишем уравнение кривой линии, по которой движется точка
, окончательно запишем уравнение кривой линии, по которой движется точка 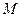 , именно
, именно 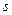 :
: 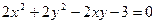 .
.
Ответ: уравнение кривой линии 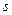 :
: 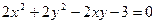 .
.
☺ ☻ ☺
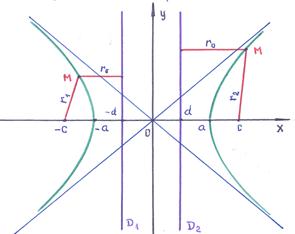 Гипербола: геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами:
Гипербола: геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами:
Пусть фокусы гиперболы располагаются на оси 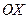 , причём:
, причём: 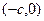 =
=  – левый фокус,
– левый фокус, 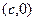 =
= 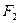 – правый фокус. Каноническое уравнение гиперболы имеет вид:
– правый фокус. Каноническое уравнение гиперболы имеет вид: 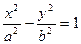 , причём
, причём  <
< 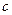 и
и 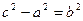 . Эксцентриситет гиперболы:
. Эксцентриситет гиперболы: 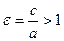 . Фокальные расстояния определяются выражениями:
. Фокальные расстояния определяются выражениями:
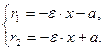 – левая ветвь → (
– левая ветвь → ( –
–  ) =–2
) =–2  .
.
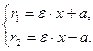 – правая ветвь → (
– правая ветвь → (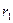 –
– 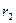 ) =2
) =2  .
.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1430; Нарушение авторских прав?; Мы поможем в написании вашей работы!