
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 8. Поверхности 2-го порядка. Канонические уравнения поверхностей 2-го порядка
|
|
|
|
☺ ☻ ☺
Пример 1 – 346: Установить, какой геометрический образ определяется заданным уравнением: 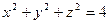 .
.
Решение:
1). Задано каноническое уравнение сферы.
2). Центр сферы находится в начале координат (0,0,0). Радиус сферы: 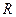 =2.
=2.
Ответ: сфера с центром в точке (0,0,0), радиуса 2.
Пример 2 – 372: Установить, какой геометрический образ определяется заданным уравнением: 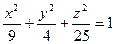 . Сделать рисунок.
. Сделать рисунок.
Решение:
1). Задано каноническое уравнение трёхосного эллипсоида.
2). Центр фигуры находится в точке (0,0,0), причём:  =3,
=3,  =2,
=2, 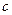 =5.
=5.
3). Выполнение рисунка заменить рассматриванием рисунка 27 в ответах задачника (внимательно посмотрите!).
Ответ: трёхосный эллипсоид с центром в точке (0,0,0), при:  =3,
=3,  =2,
=2, 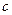 =5.
=5.
Пример 3 – 374: Установить, какой геометрический образ определяется заданным уравнением: 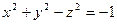 . Сделать рисунок.
. Сделать рисунок.
Решение:
1). Задано каноническое уравнение двуполостного гиперболоида вращения, ось вращения 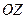 .
.
2). Центр геометрической фигуры находится в точке (0,0,0). При этом:  =
=  =
= 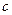 =1.
=1.
3). Выполнение рисунка заменить рассматриванием рисунка 28 б) в ответах задачника (внимательно посмотрите!).
Ответ: двуполостный гиперболоид вращения с центром (0,0,0), при  =
=  =
= 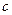 =1.
=1.
Пример 4 – 376: Установить, какой геометрический образ определяется заданным уравнением: 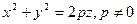 . Сделать рисунок.
. Сделать рисунок.
Решение:
1). Задано каноническое уравнение параболоида вращения, ось вращения 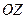 .
.
2). Центр геометрической фигуры находится в точке (0,0,0), причём:  =
=  =1,
=1,  =
=  .
.
3). Выполнение рисунка заменить рассматриванием рисунка 30 а) в ответах задачника (внимательно посмотрите!).
Ответ: параболоид вращения: центр в точке (0,0,0);  =
=  =1 и
=1 и  не определено.
не определено.
Пример 5 – 378: Установить, какой геометрический образ определяется заданным уравнением: 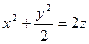 . Сделать рисунок.
. Сделать рисунок.
Решение:
1). Имеем каноническое уравнение эллиптического параболоида, ось вращения 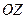 .
.
2). Центр геометрической фигуры в точке (0,0,0), При этом:  =1,
=1,  =
= 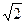 и
и  =1.
=1.
3). Выполнение рисунка заменить рассматриванием рисунка 30 а) в ответах задачника (внимательно посмотрите!).
Ответ: эллиптический параболоид, центр в точке (0,0,0), при:  =1,
=1,  =
= 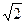 и
и  =1.
=1.
Пример 6 – 380: Установить, какой геометрический образ определяется заданным уравнением: 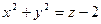 . Сделать рисунок.
. Сделать рисунок.
Решение:
1). Задано уравнение параболоида вращения, ось вращения 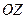 .
.
2). Центр геометрической фигуры в точке (0,0,2), при этом:  =
=  =1 и
=1 и  =
= 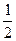 .
.
3). Выполнение рисунка заменить рассматриванием рисунка 30 а) в ответах задачника (внимательно посмотрите!).
Ответ: параболоид вращения с центром в точке (0,0,2), при:  =
=  =1 и
=1 и  =
= 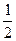 .
.
Пример 7 – 382: Установить, какой геометрический образ определяется заданным уравнением: 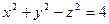 . Сделать рисунок.
. Сделать рисунок.
Решение:
1). Перепишем уравнение: 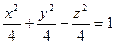 – это каноническое уравнение однополостного гиперболоида вращения, ось вращения
– это каноническое уравнение однополостного гиперболоида вращения, ось вращения 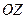 .
.
2). Центр геометрической фигуры находится в точке (0,0,0), При этом:  =
=  =
= 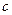 =2.
=2.
3). Выполнение рисунка заменить рассматриванием рисунка 28 а) в ответах задачника (внимательно посмотрите!).
Ответ: однополостный гиперболоид вращения с центром (0,0,0), при:  =
=  =
= 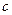 =2.
=2.
Пример 8 – 396: Установить, какой геометрический образ определяется заданным уравнением: 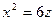 . Сделать рисунок.
. Сделать рисунок.
Решение:
1). Задано каноническое уравнение параболического цилиндра, образующая параллельна 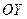 .
.
2). Центр геометрической фигуры находится в точке (0,0,0), При этом:  =3.
=3.
3). Выполнение рисунка заменить рассматриванием рисунка 31 в) с соответствующей заменой оси 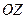 на ось
на ось 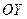 (только по-честному!).
(только по-честному!).
Ответ: параболический цилиндр,  =3.
=3.
•◄ Дополнительно ►•
Пример 9 – 371. Составить уравнение окружности, проходящей через три точки:  =(3,–1,–2),
=(3,–1,–2), 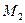 =(1,1,–2) и
=(1,1,–2) и 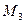 =(–1,3,0).
=(–1,3,0).
 Решение:
Решение:
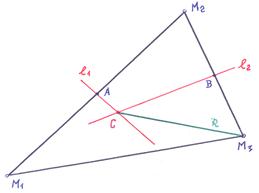
Алгоритм:
1) строим серединные перпендикуляры к сторонам треугольника 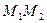 и
и 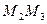 в виде прямых линий
в виде прямых линий  и
и  ;
;
2) находим центр окружности  =
= 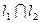 ;
;
3) вычисляем радиус 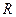 окружности и сферы, которая будет содержать искомую окружность;
окружности и сферы, которая будет содержать искомую окружность;
4) находим уравнение сферы радиуса 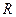 с центром в точке
с центром в точке  и уравнение плоскости, содержащей заданные точки
и уравнение плоскости, содержащей заданные точки 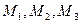 ;
;
5) строим систему уравнений для сферы и плоскости – это и будет искомая окружность в пространстве  .
.
Реализуем принятый алгоритм:
1). Найдём координаты точек  и
и  . Из равенства
. Из равенства 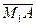 =
= 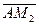 получаем
получаем  (2,0,–2), из равенства
(2,0,–2), из равенства 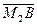 =
= 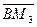 получаем
получаем  (0,2,–1). Для прямых
(0,2,–1). Для прямых  и
и  строим векторы нормалей:
строим векторы нормалей: 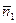 =
= 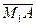 =(–1,1,0),
=(–1,1,0), 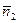 =
= 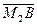 =(–1,1,1). Запишем уравнение
=(–1,1,1). Запишем уравнение  :
: 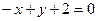 , также запишем
, также запишем  :
: 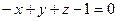 .
.
2). Находим координаты точки  из системы:
из системы: 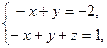 откуда
откуда  (2,0,3).
(2,0,3).
3). Вычисляем радиус окружности (и сферы): 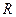 =
= 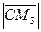 =
= 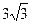 . Записываем уравнение сферы с центром в точке
. Записываем уравнение сферы с центром в точке  радиуса
радиуса 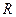 :
: 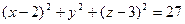 .
.
4). Строим вектор нормали плоскости  , содержащей заданные точки:
, содержащей заданные точки: 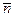 =
= 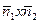 =
= 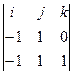 , или
, или 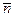 =(1,1,0). Записываем уравнение
=(1,1,0). Записываем уравнение  с учётом условия
с учётом условия 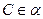 , именно
, именно  :
: 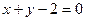 .
.
5). Записываем уравнение окружности в пространстве: 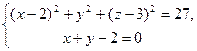 как пересечение плоскости со сферой.
как пересечение плоскости со сферой.
Ответ: окружность в пространстве: 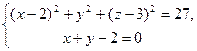 .
.
☻
Вопросы для самопроверки:
1. Как получают поверхности вращения 2-го порядка?
2. Как получают канонические уравнения поверхностей 2-го порядка?
3. Как применяют «метод сечений» для исследования поверхностей 2-го порядка?
4. Что такое «гиперболический параболоид», как получают его уравнение?
5. Мог ли инженер Гарин, используя гиперболоид, плавить руду и добывать золото?
6. Чем примечательна конструкция Останкинской телебашни?
< * * * * * >
Задачи для самоподготовки:
Пример C8 – 1: Установить, какой геометрический образ определяется заданным уравнением: 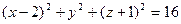 .
.
Ответ: сфера с центром в точке (2,0,–1), радиуса 4.
Пример C8 – 2: Установить, какой геометрический образ определяется заданным уравнением: 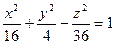 . Сделать рисунок.
. Сделать рисунок.
Ответ: однополостный гиперболоид с центром в точке (0,0,0), при:  =4,
=4,  =2,
=2, 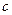 =6.
=6.
Пример C8 – 3: Установить, какой геометрический образ определяется заданным уравнением: 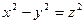 . Сделать рисунок.
. Сделать рисунок.
Ответ: конус вращения с центром в точке (0,0,0), при  =
=  =
= 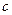 =1.
=1.
Пример C8 – 4: Установить, какой геометрический образ определяется заданным уравнением: 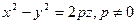 . Сделать рисунок.
. Сделать рисунок.
Ответ: параболоид гиперболический с центром (0,0,0), при:  =
=  =1 и
=1 и  не определено.
не определено.
Пример C8 – 5: Установить, какой геометрический образ определяется заданным уравнением: 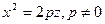 . Сделать рисунок.
. Сделать рисунок.
Ответ: параболический цилиндр, образующая параллельна 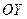 ,
,  не определено.
не определено.
Пример C8 – 6: Установить, какой геометрический образ определяется заданным уравнением: 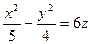 . Сделать рисунок.
. Сделать рисунок.
Ответ: параболоид гиперболический с центром (0,0,0), при:  =
= 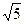 ,
,  =2 и
=2 и  =3.
=3.
Пример C8 – 7: Установить, какой геометрический образ определяется заданным уравнением: 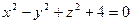 . Сделать рисунок.
. Сделать рисунок.
Ответ: двуполостный гиперболоид вращения с центром в точке (0,0,0), при:  =
=  =
= 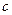 =2.
=2.
Пример C8 – 8: Установить, какой геометрический образ определяется заданным уравнением: 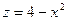 . Сделать рисунок.
. Сделать рисунок.
Ответ: параболический цилиндр, образующая параллельна 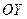 ,
,  =–
=– 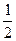 .
.
< * * * * * >
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1047; Нарушение авторских прав?; Мы поможем в написании вашей работы!