Назначение критерия. Методические рекомендации к изучению темы

Материалы лекции

Методические рекомендации к изучению темы

При изучении данной темы необходимо учесть то, что критерии являются непараметрическими, они оперируют частотами абсолютными или процентными. Обратите особое внимание на правила принятия решения для рассмотренных критериев: эти правила могут быть противоположны. Внимательно изучите ограничения в применении критериев.

После изучения материала лекции ответьте на контрольные вопросы, ответы занесите в конспект. При самостоятельном изучении биномиального критерия материал в конспекте должен быть изложен в следующей последовательности: назначение критерия, ограничения в его использовании, алгоритм расчета критерия с указанием правила принятия решения.

Многофункциональные статистические критерии — это критерии, которые могут использоваться по отношению к самым разнообразным данным, выборкам и задачам. Это означает, что данные могут быть представлены в любой шкале, начиная от шкалы наименований. Выборки могут быть как зависимыми, так и независимыми. Эти критерии позволяют решать задачи сравнения уровней выраженности признака, оценки сдвигов значений и сравнения распределений.

Многофункциональные критерии построены на сопоставлении долей, выраженных в долях единицы или в процентах. Суть критериев состоит в определении того, какая доля наблюдений (реакций, выборов, испытуемых) в данной выборке характеризуется интересующим исследователя эффектом и какая доля этим эффектом не характеризуется.

Критерий φ * применяется в тех случаях, когда обследованы две выборки испытуемых, биномиальный критерий m — в тех случаях, когда обследована лишь одна выборка испытуемых.

Критерий φ* — «Угловое преобразование» Фишера

Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.

Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект.

Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол φ, а меньшей доле – меньший угол, но соотношения здесь не линейные: 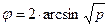, где р — процентная доля, выраженная в долях единицы (см. рис. 18).

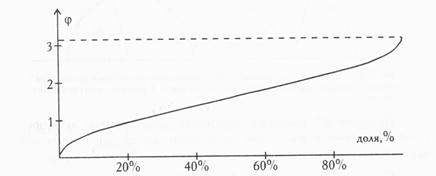
Рис. 18. График зависимости угла φ от процентной доли

При увеличении расхождения между углами φ₁ и φ₂ и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.

Ограничения критерия φ*

1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ* в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным.

2. Верхний предел в критерии φ* отсутствует — выборки могут быть сколь угодно большими.

Нижний предел — 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:

а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30:

N₁=2 ® N₂≥30

б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7:

N₁=3 ® N₂≥7

в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5:

N₁=4 ® N₂≥5

г) при N₁, N₂≥5 возможны любые сопоставления.

В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением N₁=2 и N₂=15, но в этих случаях не удастся выявить достоверных различий.

Других ограничений у критерия φ* нет.

Алгоритм расчета критерия φ*

1. Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта». Если признак измерен количественно, использовать критерий λ для поиска оптимальной точки разделения.

2. Начертить четырехклеточную таблицу (таблица 23) из двух столбцов и двух строк. Первый столбец - «есть эффект»; второй столбец - «нет эффекта»; первая строка сверху – 1 группа (выборка); вторая строка – 2 группа (выборка).

Таблица 23

Выборка	«Есть эффект»	«Нет эффекта»	Σ
1 выборка
2 выборка
Σ

3. Подсчитать количество испытуемых в первой группе, у которых «есть эффект», и занести это число в левую верхнюю ячейку таблицы.

4. Подсчитать количество испытуемых в первой выборке, у которых «нет эффекта», и занести это число в правую верхнюю ячейку таблицы. Подсчитать сумму по двум верхним ячейкам. Она должна совпадать с количеством испытуемых в первой группе.

5. Подсчитать количество испытуемых во второй группе, у которых «есть эффект», и занести это число в левую нижнюю ячейку таблицы.

6. Подсчитать количество испытуемых во второй выборке, у которых «нет эффекта», и занести это число в правую нижнюю ячейку таблицы. Подсчитать сумму по двум нижним ячейкам. Она должна совпадать с количеством испытуемых во второй группе (выборке).

7. Определить процентные доли испытуемых, у которых «есть эффект», путем отнесения их количества к общему количеству испытуемых в данной группе (выборке). Записать полученные процентные доли соответственно в левой верхней и левой нижней ячейках таблицы в скобках, чтобы не перепутать их с абсолютными значениями.

8. Проверить, не равняется ли одна из сопоставляемых процентных долей нулю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно или нежелательно, от казаться от критерия φ* и использовать критерий c².

9. Определить по специальной таблице (приложение 1.7) величины углов для каждой из сопоставляемых процентных долей φ₁ и φ₂.

10. Подсчитать эмпирическое значение φ* по формуле:

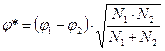
где φ* — расчетное значение критерия;

φ₁— угол, соответствующий большей процентной доле;

φ₂— угол, соответствующий меньшей процентной доле;

N₁— количество наблюдений в выборке 1;

N₂— количество наблюдений в выборке 2.

11. Правило принятия решения:

Сопоставить полученное значение φ* с критическими значениями:

φ*=1,64 на уровне значимости р=0,95 и φ*=2,31 на уровне значимости р=0,99.

Если φ*_расч> φ*_табл, то различия между сравниваемыми процентными долями статистически значимы.

Если φ*_расч≤ φ*_табл, то различия между сравниваемыми процентными долями статистически незначимы.

Дата добавления: 2014-12-26