Однофакторный дисперсионный анализ

В данной теме будет рассмотрен только однофакторный дисперсионный анализ, используемый для несвязанных выборок. Оперируя как основным понятием дисперсии, этот анализ базируется на расчете дисперсий трех типов:

• общая дисперсия, вычисленная по всей совокупности экспериментальных данных;

• внутригрупповая дисперсия, характеризующая вариативность признака в каждой выборке;

• межгрупповая дисперсия, характеризующая вариативность групповых средних.

Основное положение дисперсионного анализа гласит: общая дисперсия равна сумме внутригрупповой и межгруппповой дисперсий.

Это положение можно записать в виде уравнения:

где х_ij — значения всех переменных, полученных в эксперименте; при этом индекс j меняется от 1 до р, где р — число сравниваемых выборок, их может быть три и больше; индекс i соответствует числу элементов в выборке (их может быть два и больше);

— общая средняя всей анализируемой совокупности данных;

— средняя j выборки;

N — общее число всех элементов в анализируемой совокупности экспериментальных данных;

р — число экспериментальных выборок.

Проанализируем это уравнение более подробно.

Пусть у нас имеется р групп (выборок). В дисперсионном анализе каждую выборку представляют в виде одного столбца (или строки) чисел. Тогда, для того чтобы можно было указать на конкретную группу (выборку), вводится индекс j, который меняется соответственно от j = 1 до j = р. Например, если у нас 5 групп (выборок), то р=5, а индекс j меняется соответственно от j= 1 до j= 5.

Пусть перед нами стоит задача — указать конкретный элемент (значение измерения) какой-либо выборки. Для этого мы должны знать номер этой выборки, например 4, и расположение элемента (измеренного значения) в этой выборке. Этот элемент может располагаться в выборке начиная с первого значения (первая строчка) до последнего (последняя строчка). Пусть наш искомый элемент расположен на пятой строчке. Тогда его обо значение будет таково: х₅₄. Это значит, что выбран пятый элемент в строчке из четвертой выборки.

В общем случае в каждой группе (выборке) число составляющих ее элементов может быть различным — поэтому обозначим число элементов в j группе (выборке) через n_j. Полученные в эксперименте значения признака в j группе обозначим через х_ij, где i = 1, 2,... n — порядковый номер наблюдения в j группе.

Дальнейшие рассуждения целесообразно проводить с опорой на таблицу 25. Отметим, однако, что для удобства дальнейших рассуждений, выборки в этой таблице представлены не как столбцы, а как строчки (что, однако, не принципиально).

В итоговой, последней строке таблицы даны: общий объем всей выборки — N, сумма всех полученных значений G и общая средняя всей выборки . Эта общая средняя получена как сумма всех элементов анализируемой совокупности экспериментальных данных, обозначенная выше как G, деленная на число всех элементов N.

В крайнем правом столбце таблицы представлены величины средних по всем выборкам. Например, в j выборке (строчка таблицы обозначенная символом j) величина средней (по всей j выборке) такова:

Таблица 25

Номер выборки	Полученные значения признака	Число элементов в каждой выборке	Сумма всех элементов выборки	Средняя по выборке
	Х11, х21…, хn11	n1	Sxi1 = T1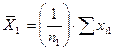
…..	…..	…..	…..	…..
j	х1j, х2j…, хni,j	nj	Sxij = Tj
…..	…..	…..	…..	…..
p	Х1p, х2p…, хnp,p	np	Sхip = Tp
Итого		N = Snj	SSxij = G

Для расчета по методу однофакторного дисперсионного анализа, согласно уравнению рассмотренному выше, необходимо определить две дисперсии: межгрупповую (дисперсию групповых средних) и внутригрупповую, поскольку общая дисперсия всей выборки является суммой этих дисперсий.

Считается, что межгрупповая дисперсия обусловлена влиянием изучаемого фактора, а величина внутригрупповой дисперсии рассматривается как случайная.

Подчеркнем, однако, что при расчетах по методу однофакторного дисперсионного анализа, вначале подсчитываются не дисперсии, а квадраты отклонений (которые представлены в числителях всех трех членов рассмотренной выше основной формулы дисперсионного анализа) и лишь в заключительной части расчетов они делятся на соответствующие величины для получения дисперсий и их дальнейшего сравнения.

Таким образом, в терминах квадратов отклонений основное уравнение однофакторного дисперсионного анализа можно переписать так:

Общая сумма квадратов отклонений = сумма квадратов отклонений от групповых средних + сумма квадратов отклонений групповых средних от общей средней.

Перепишем это положение в виде второго уравнения:

Q_o = Q₁ + Q₂,

где: Q_o — общая сумма квадратов отклонений;

Q₁ — сумма квадратов отклонений от групповых средних;

Q₂ — сумма квадратов отклонений групповых средних от общей средней.

Теперь эти же обозначения представим в виде расчетных формул:

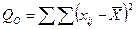
Для получения дисперсии необходимо поделить каждую из этих величин на соответствующую величину степеней свободы.

Пусть 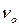— число степеней свободы, учитываемое при расчете общей дисперсии, 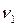— число степеней свободы, учитываемое при расчете внутригрупповой дисперсии (согласно первому уравнению оно равно N – p), — число степеней свободы, учитываемое при расчете межгрупповой дисперсии (согласно первому уравнению оно равно p–1).

Тогда 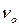= 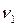+ = N – p + p – 1 = N – 1, и вычисление оценок дисперсий будет осуществляться таким образом:

и

Дисперсия S₁² — характеризует рассеяние внутри групп (случайная вариация признака), эту величину называют также остаточной дисперсией.

Дисперсия S₂² — характеризует рассеяние групповых средних (систематическая вариация).

Заключительным этапом дисперсионного анализа является вычисление отношения дисперсий по формуле следующей формуле:

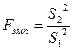
При этом межгрупповая дисперсия S₂² всегда находится в числителе, а внутригрупповая S₁² (случайная) — в знаменателе.

Оценка уровня значимости статистической гипотезы в дисперсионном анализе осуществляется с помощью F критерия Фишера.

Правило вывода:

По таблице критических значений критерия Фишера (см. приложение 1.3) в зависимости от числа степеней свободы находим критические значения критерия Фишера.

Если влияние фактора отсутствует, то вычисленное отношение не превзойдет критический предел (F_эмп. £ F_крит.), тогда следует принять нулевую гипотезу Н₀ об отсутствии влияний фактора на экспериментальные данные.

Напротив, если влияние фактора велико, то (F_эмп. > F_крит.), в этом случае необходимо принять альтернативную гипотезу Н₁ о наличии влияния фактора на экспериментальные данные.

В дисперсионном анализе нулевую гипотезу Н₀ можно сформулировать так: средние величины анализируемого результативного фактора одинаковы для всех его градаций. Соответственно альтернативная гипотеза Н₁ будет утверждать, что средние величины результативного фактора различны для всех его градаций.

Поскольку для дисперсионного анализа необходимо получить общую сумму квадратов отклонений (обозначаемую как Q_o), то согласно определению дисперсии необходимо из каждого элемента экспериментальной совокупности данных вычесть общее среднее, полученные величины возвести в квадрат и сложить. Поскольку подобную вычислительную процедуру проделать достаточно сложно, то для вычислений по методу однофакторного дисперсионного анализа используются более простые уравнения.

При этом расчет оценок дисперсий удобно проводить по специальной таблице, получившей название таблицы дисперсионного анализа (таблица 26).

Таблица 26

Характер вариации	Сумма квадратов	Число степеней свободы	Оценка дисперсии
Межгрупповая		p – 1
Внутригрупповая		N – p
Итого		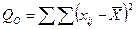N – 1

При этом величины Q_o, Q₁ и Q₂ можно вычислить по следующим упрощенным формулам:

Поскольку Q₁ = Q_О – Q₂ , то

Для применения однофакторного дисперсионного анализа (как, кстати, и любого другого дисперсионного анализа) необходимо соблюдать следующие условия:

1. Измерение должно быть произведено в шкале равных интервалов (интервальной) или равных отношений (пропорциональной).

2. Результативный признак должен быть распределен нормально в исследуемой выборке.

3. Для адекватного использования метода требуется не менее трех градаций фактора и не менее двух испытуемых в каждой градации.

Контрольные вопросы:

1. Основное назначение дисперсионного анализа?

2. Каким условиям должны отвечать исходные данные для применения дисперсионного анализа?

3. Как оценить нормальность распределения признака в выборке?

4. В чем заключается различие двух видов дисперсионного анализа — однофакторного и двухфакторного?

5. Каковы основные этапы выполнения однофакторного дисперсионного анализа?

Самостоятельное практическое задание:

1. Самостоятельно изучите особенности дисперсионного анализа для зависимых выборок и запишите алгоритм его проведения.

2. Самостоятельно изучите двух факторный дисперсионный анализ и запишите алгоритмы его проведения для независимых и зависимых выборок.

Материалы для изучения темы:

а) основная литература:

1. Ермолаев О. Ю. Математическая статистика для психологов. — М., 2008. — Стр. 178-201.

2. Кутейников А.Н. Математические методы в психологии. – СПб, 2008. — Стр. 114-133.

3. Наследов А. Д. Математические методы психологического исследования: Анализ и интерпретация данных. — СПб., 2007. — Стр. 185-234.

4. Сидоренко Е. В. Методы математической обработки в психологии. — СПб.,2004. — Стр. 224-260.

б) дополнительная литература:

1. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии. — М., 1976. — Стр. 305-342; 259-436.

2. Суходольский Г. В. Основы математической статистики для психологов. — СПб., 1998. — Стр. 340-372.

Дата добавления: 2014-12-26