Ограничения критерия. Критерий «хи-квадрат» Пирсона

Описание критерия

Назначения критерия

Критерий «хи-квадрат» Пирсона

Критерий хи-квадрат Пирсона был рассмотрен в теме № 6. Напомним его назначение, сущность и ограничения в применении.

Критерий χ² применяется в двух целях;

1) для сопоставления эмпирического распределения признака с теоре­тическим (равномерным, нормальным или каким-то иным);

2) для сопоставления двух, трех или более эмпирических распределе­ний одного и того же признака, то есть для проверки их однородности;

3) для оценки стохастической (вероятностной) независимости в системе случайных событий;

и т.д.

Критерий χ² отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях.

Преимущество метода состоит в том, что он позволяет сопостав­лять распределения признаков, представленных в любой шкале, начиная от шкалы наименований. В самом простом случае альтерна­тивного распределения ("да - нет", "допустил брак - не допустил бра­ка", "решил задачу - не решил задачу" и т. п.) мы уже можем приме­нить критерий χ².

1. Объем выборки должен быть достаточно большим: N>30. При N<30 критерий χ² дает весьма приближенные значения. Точность крите­рия повышается при больших N.

2. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: f ≥ 5. Это означает, что если число разрядов задано зара­нее и не может быть изменено, то мы не можем применять метод χ², не накопив определенного минимального числа наблюдений. Ес­ли, например, мы хотим проверить наши предположения о том, что частота обращений в телефонную службу Доверия неравномерно распределяются по 7 дням недели, то нам потребуется 5-7=35 обра­щений. Таким образом, если количество разрядов (k) задано зара­нее, как в данном случае, минимальное число наблюдений (N_min) оп­ределяется по формуле: .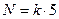

3. Выбранные разряды должны "вычерпывать" все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопостав­ляемых распределениях.

4. Необходимо вносить "поправку на непрерывность" при сопоставле­нии распределений признаков, которые принимают всего 2 значения. При внесении поправки значение χ², уменьшается (см. пример с по­правкой на непрерывность).

5. Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду. Сумма наблюдений по разрядам всегда должна быть равна общему количеству наблюдений.

Алгоритм расчета критерия и правило вывода не изменяются. Поэтому подробно на этом критерии в данной теме мы останавливаться не будем.

Дата добавления: 2014-12-26