Коэффициент взаимной сопряженности Чупрова

Коэффициент взаимной сопряженности Чупрова К является мерой связи двух признаков, если один из них измерен по шкале наименований и может иметь несколько значений (больше двух), а второй признак измерен по такой же шкале или по шкале порядка, или по шкале интервальной, или по шкале пропорциональной.

Этот коэффициент рассчитывается с помощью критерия хи-квадрат Пирсона, расчетное значение которого подставляется в формулу:

при k≠m, где k — число градаций одного признака, m — число градаций значений другого признака

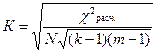
при k=m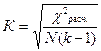

Таблиц с критическими значениями для коэффициента взаимной сопряженности Чупрова не существует. Поэтому поступают следующим образом:

1. Вычисляют расчетное значение критерия хи-квадрат Пирсона. Обратите внимание на то, что ограничения в использовании этого коэффициента соответствуют ограничениям критерия хи-квадрат Пирсона, а именно: объем выборки должен быть N≥30 и теоретическая частота в ячейках должна быть f≥ 5.

2. Сравнивают его с критическим значением критерия хи-квадрат Пирсона для соответствующего числа степеней свободы (см. приложение 1.6).

3. Если χ²_расч < χ²_табл, то расхождения между рас­пределениями статистически недостоверны, или признаки изменяются несогласованно, или связи между признаками нет. Делается вывод об отсутствии взаимосвязи. Величину коэффициента К можно в этом случае не вычислять.

4. Если χ²_расч ≥ χ²_табл, то рас­хождения между распределениями статистически достоверны, или признаки изменяются согласованно, или связь между признаками статистически значима.

5. Далее вычисляется значение коэффициента взаимной сопряженности Чупрова, которое и является мерой связи. Чем больше это значение по абсолютной величине, тем сильнее взаимосвязь. Напоминаю, что знак коэффициента взаимной сопряженности Чупрова не интерпретируется, так как он не указывает на направление взаимосвязи, потому что зависит от обозначений градаций значений признака.

Дата добавления: 2014-12-26