
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бисериальные коэффициенты корреляции
|
|
|
|
Бисериальные коэффициенты корреляции оценивают зависимость между двумя признаками, один из которых измерен в шкале наименований с двумя градациями признака (дихотомической шкале). Бисериальные коэффициенты корреляции изменяются в диапазоне от -1 до +1, однако следует помнить, что в данном случае знак для интерпретации не имеет значения (это исключение из общего правила).
Рангово-бисериальный коэффициент корреляции используется в том случае, когда второй признак измерен по шкале порядка.
Расчет этого коэффициента производится по формуле:
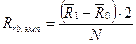
где 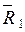 — средний ранг по тем элементам переменной Y, которым соответствует код 1 в переменной X;
— средний ранг по тем элементам переменной Y, которым соответствует код 1 в переменной X;
 — средний ранг по тем элементам переменной Y, которым соответствует код 0 в переменной X;
— средний ранг по тем элементам переменной Y, которым соответствует код 0 в переменной X;
N — общее количество испытуемых.
Оценку значимости рангово-бисериального коэффициента корреляции произведем с помощью критерия Стьюдента.
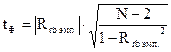
где 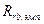 — расчетное значение рангово-бисериального коэффициента корреляции;
— расчетное значение рангово-бисериального коэффициента корреляции;
N — число испытуемых;
tФ — расчетное значение критерия Стьюдента.
Расчеты рангово-бисериального коэффициента корреляции целесообразно вести в следующей таблице (таблица 28):
Таблица 28
| хi | yi | Ri | R1 | R0 |
| y1 | R1 | R1 | ||
| y2 | R2 | R2 | ||
| y3 | R3 | R3 | ||
| y4 | R4 | R4 | ||
| y5 | R5 | R5 | ||
| y6 | R6 | R6 | ||
| …… | …… | …… | …… | …… |
| yN | RN | RN | ||
| ∑R1 | ∑R0 |
Правило принятия решения:
Табличное значение критерия Стьюдента находится по таблице критических значений в зависимости от числа степеней свободы (см. приложение 1.2). Число степеней свободы k=N-2.
Если расчетное значение критерия tФ≥ tтабл ., то между признаками существует статистическая значимая связь.
Если расчетное значение критерия tФ≤ tтабл ., то между признаками статистической связи нет.
Бисериальный коэффициент корреляциииспользуется в том случае, когда второй признак измерен по шкале равных интервалов или шкале равных отношений. Расчет этого коэффициента производится по формуле:

где 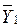 — среднее значение по тем элементам переменной Y, которым соответствует код 1 в переменной X;
— среднее значение по тем элементам переменной Y, которым соответствует код 1 в переменной X;
n1 — количество значений 1 в переменной Х;
 — среднее значение по тем элементам переменной Y, которым соответствует код 0 в переменной X;
— среднее значение по тем элементам переменной Y, которым соответствует код 0 в переменной X;
n0 — количество значений 0 в переменной Х;
Sx — стандартное отклонение переменной Y;
N — общее количество испытуемых (N=n1+n0).
Оценку значимости рангово-бисериального коэффициента корреляции произведем с помощью критерия Стьюдента.
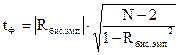
где 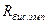 — расчетное значение бисериального коэффициента корреляции;
— расчетное значение бисериального коэффициента корреляции;
N — число испытуемых;
tФ — расчетное значение критерия Стьюдента.
Расчеты бисериального коэффициента корреляции целесообразно вести в таблице следующего вида (таблица 29):
Таблица 29
| хi | yi | yi– 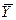
| (yi– 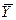 )2 )2
| yi1 | yi0 |
| y1 | y1 | ||||
| y2 | y2 | ||||
| y3 | y3 | ||||
| y4 | y4 | ||||
| y5 | y5 | ||||
| y6 | y6 | ||||
| …… | …… | …… | …… | ||
| yN | RN | ||||
| ∑yi | ∑(yi– 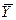 )2 )2
| ∑y1 | ∑y0 |
Правило принятия решения:
Табличное значение критерия Стьюдента находится по таблице критических значений в зависимости от числа степеней свободы (см. приложение 1.2). Число степеней свободы k=N-2.
Если расчетное значение критерия tФ≥ tтабл ., то между признаками существует статистическая значимая связь.
Если расчетное значение критерия tФ≤ tтабл ., то между признаками статистической связи нет.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1001; Нарушение авторских прав?; Мы поможем в написании вашей работы!