
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм расчет критерия
|
|
|
|
Ограничения в использовании критерия
Назначение критерия
Критерий Макнамары
Критерий Макнамары очень прост, однако его использование имеет некоторые особенности и требует определенных навыков в статистических расчетах и работе с таблицами критических величин. Этот критерий относится также к числу непараметрических критериев и предназначен для работы с данными, полученными в самой простой из номинальных в дихотомической шкале. Критерий позволяет оценить различия между значениями признака, полученные в двух замерах на одной и той же выборке испытуемых.
Для применения критерия Макнамары необходимо соблюдать следующие условия:
1. Измерение должно быть проведено дихотомической шкале (в шкале наименований, при этом признак может иметь всего два значения).
2. Выборка должна быть зависимой.
1. На основании первичных данных составляется 4-хклеточная таблица следующего вида (таблица 24).
Таблица 24
| Замеры | Второй замер | Σ | ||
| Значения признака | Первый вариант ответа | Второй вариант ответа | ||
| Первый замер | Первый вариант ответа | A=f11 | B=f12 | A+B=f1– |
| Второй вариант ответа | C=f21 | D=f22 | C+D=f2– | |
| Σ | A+C=f11 | B+D=f11 | N |
В таблице 34 «А» обозначает число испытуемых, которые в первый и второй замеры выбрали первый вариант ответа; «С» — число испытуемых, которые в первый замер выбрали второй вариант ответа, а во второй замер выбрали первый вариант ответа; «В» — число испытуемых, которые в первый замер выбрали первый вариант ответа, а во второй замер — второй вариант ответа; «D» — число испытуемых, которые оба раза (в первый и второй замеры) выбрали второй вариант ответа.
Возможна ситуация, в которой В = С. В этом случае критерий Макнамары не может быть применен и следует воспользоваться критерием хи-квадрат.
2. Работа по критерию Макнамары начинается с выяснения вопроса о том, будет ли сумма чисел, стоящих в ячейках В и С, меньше или равна 20 или эта сумма будет превышать число 20. В первом случае, то есть когда сумма чисел В+С ≤ 20 используется один способ расчета по критерию — способ А. Если сумма чисел, стоящих в ячейках В + С > 20 — используется другой способ, способ Б.
Способ А. Пусть сумма (В + С) ≤ 20, тогда дальнейший расчет по критерию Макнамары производится следующим образом:
3. Находится наименьшая величина из величин В и С, которая обозначается буквой m, т.е т m=min (В или С).
3. Находится сумма величина В + С, которая обозначается буквой n, т.е. n= В + С.
4. По таблице приложения в данном пособии (таблицы критических значений биномиального распределения — приложение 1.8) на пересечении строк и столбцов таблицы m и n находится величина Мэмп.. Особо подчеркнем, что, в отличие от всех критериев, по таблице приложения 10 находятся не критические величины, а именно эмпирическое значение критерия Макнамары. Это принципиальное отличие этого критерия от всех других.
Примечание. Нули в таблице приложения 1.8 опущены, поэтому к любому числу, найденному по этой таблице, нужно слева добавить нуль и занятую, так чтобы получить необходимую величину в виде: 0,«число, взятое из таблицы».
5. Правило вывода:
Величины Мкрит. в случае способа А являются постоянными и равны соответственно Мкрит.=0,025 для 5% уровня значимости и Мкрит.=0,005 для 1% уровня значимости.
Если Мэмп. ≤ Мкрит., различия между замерами статистически значимы.
Если Мэмп. > Мкрит., различия между замерами статистически незначимы.
Способ Б. Пусть сумма (В + С) > 20.
3. Производится расчет Мэмп. по следующей формуле:
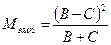
4. Правило вывода:
Находятся критические величины Мкрит. по таблице критических значений для критерия хи-квадрат с числом степеней свободы ν=1(для четырехпольных таблиц). Однако поскольку величина степени свободы критерия хи-квадрат в данном случае всегда постоянна и равна 1, то критические величины Мкрит. так же, как и в случае способа А, всегда одни и те же и равны Мкрит. =3,841 для 5% уровня значимости и Мкрит. = 6,635 для 1% уровня значимости.
Если Мэмп. ≥ Мкрит., различия между замерами статистически значимы.
Если Мэмп. < Мкрит., различия между замерами статистически незначимы.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 3961; Нарушение авторских прав?; Мы поможем в написании вашей работы!