Материалы лекции

⇐ Предыдущая 48 49 50 515253 54 55 56 57 Следующая ⇒

Методические рекомендации к изучению темы

Тема 11. Анализ структуры взаимосвязей

Корреляционные матрицы. Графический метод анализа корреляционной матрицы. Метод корреляционных плеяд. Понятие графов. Ориентированный граф. Мощность плеяды. Крепость плеяды. Типы структур: цепь, кольцо, звезда, решетка.

Максимальный корреляционный путь как аналог однофакторного решения Спирмена (центроидный метод). Анализ корреляционной матрицы методом построения максимального корреляционного пути. Алгоритм построения максимального корреляционного пути.

При изучении темы таблицу 1 необходимо выучить наизусть, это поможет в дальнейшем выбирать меры оценки взаимосвязей, адекватные данному конкретному случаю. Обратите внимание на то, что пользование данной таблицей предполагает ответ на вопрос — по каким шкалам измерены признаки, между которыми оценивается взаимосвязь.

При работе с алгоритмами мер связи внимательно изучите возможные ограничения в применении и все шаги алгоритма.

После изучения материала лекции ответьте на контрольные вопросы, решите примеры, ответы занесите в конспект.

В реальном исследовании мы, как правило, имеем дело не с двумя признаками, а с множеством их. Результатом корреляционного анализа является матрица, в которой записаны коэффициенты корреляции, характеризующие взаимосвязи каждого признака с каждым. Удобнее такую матрицу представить в виде квадратной таблицы (таблица 35), в которой число строк и столбцов одинаково и равно числу переменных (признаков) m+1. Например, пусть m=10.

Таблица 35

Признаки
	r₁₁	r₁₂	r₁₃	r₁₄	r₁₅	r₁₆	r₁₇	r₁₈	r₁₉	r_{1 10}
	r₂₁	r₂₂	r₂₃	r₂₄	r₂₅	r₂₆	r₂₇	r₂₈	r₂₉	r_{2 10}
	r₃₁	r₃₂	r₃₃	r₃₄	r₃₅	r₃₆	r₃₇	r₃₈	r₃₉	r_{3 10}
	r₄₁	r₄₂	r₃₄	r₄₄	r₄₅	r₄₆	r₄₇	r₄₈	r₄₉	r_{4 10}
	r₅₁	r₅₂	r₃₅	r₅₄	r₅₅	r₅₆	r₅₇	r₅₈	r₅₉	r_{5 10}
	r₆₁	r₆₂	r₃₆	r₆₄	r₆₅	r₆₆	r₆₇	r₆₈	r₆₉	r_{6 10}
	r₇₁	r₇₂	r₃₇	r₇₄	r₇₅	r₇₆	r₇₇	r₇₈	r₇₉	r_{7 10}
	r₈₁	r₈₂	r₃₈	r₈₄	r₈₅	r₈₆	r₈₇	r₈₈	r₈₉	r_{8 10}
	r₉₁	r₉₂	r₉₃	r₉₄	r₉₅	r₉₆	r₉₇	r₉₈	r₉₉	r_{9 10}
	r_{10 1}	r_{10 2}	r_{10 3}	r_{10 4}	r_{10 5}	r_{10 6}	r_{10 7}	r_{10 8}	r_{10 9}	r_{10 10}

Поскольку эта матрица является симметричной относительно диагонали, выделенной жирным шрифтом, то обычно анализируется половина такой матрицы, расположенная ниже или выше выделенной диагонали (по этой диагонали находятся коэффициенты корреляции признака с самим собой: они равны 1,00) — табл. 36.

Таблица 36

Признаки
	1,00
	r₂₁	1,00
	r₃₁	r₃₂	1,00
	r₄₁	r₄₂	r₄₃	1,00
	r₅₁	r₅₂	r₅₃	r₅₄	1,00
	r₆₁	r₆₂	r₆₃	r₆₄	r₆₅	1,00
	r₇₁	r₇₂	r₃₇	r₇₄	r₇₅	r₇₆	1,00
	r₈₁	r₈₂	r₃₈	r₈₄	r₈₅	r₈₆	r₈₇	1,00
	r₉₁	r₉₂	r₉₃	r₉₄	r₉₅	r₉₆	r₉₇	r₉₈	1,00
	r_{10 1}	r_{10 2}	r_{10 3}	r_{10 4}	r_{10 5}	r_{10 6}	r_{10 7}	r_{10 8}	r_{10 9}	1,00

Далее в подобной матрице необходимо выделить те коэффициенты корреляции, которые по абсолютному значению равны или больше критического значения (табличного). И только эти коэффициенты подлежат содержательному анализу.

Для удобства такого анализа могут быть построены корреляционные плеяды.

Корреляционная плеяда представляет собой граф, являющийся одной из простейших математических моделей взаимодействующих систем, представляющий собой систему точек (вершин), некоторые из которых соединены отрезками (рёбрами). В данном случае вершинами являются признаки, а ребра отражают взаимосвязи между ними. Например, на рис. 20 изображена корреляционная плеяда, полученная в одном из дипломных исследований.

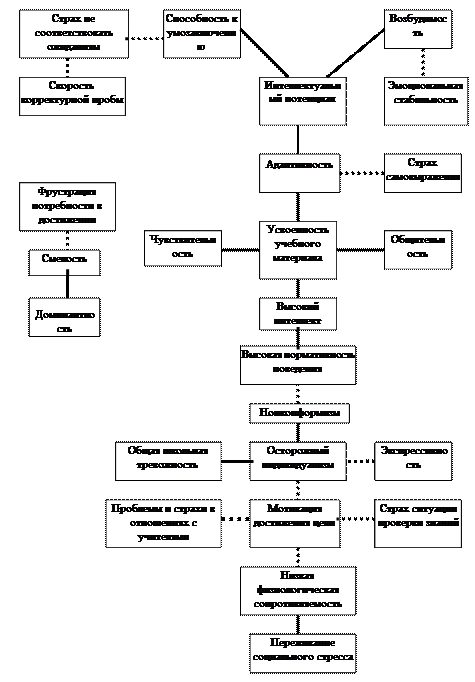
Рис.20. Корреляционная плеяда взаимосвязей признаков 9а класса

Примечание к рисунку 20: сплошной линией обозначены положительные, пунктирной линией — отрицательные корреляционные зависимости.

Таким образом, корреляционная плеяда [8](ρF-группа[9])— этоориентированный граф, вершинами которого служат психологические переменные, рёбрами – парные корреляции между ними, а ориентация любой пары вершин задаётся знаком, весом и направлением корреляции между ними.

Если корреляционную плеяду построить по методу выделения максимальных взаимосвязей между признаками (методу максимального корреляционного пути), то она является, как это было показано Б. Докторовым[10], графическим аналогом центроидного метода в классическом факторном анализе, основанным на применении теории графов к анализу корреляционной матрицы. Рассмотрим данный алгоритм[11].

⇐ Предыдущая 48 49 50 515253 54 55 56 57 Следующая ⇒

Поделиться с друзьями:

Дата добавления: 2014-12-26; Просмотров: 809; Нарушение авторских прав?; Мы поможем в написании вашей работы!

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

studopedia.su - Студопедия (2013 - 2025) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление

Генерация страницы за: 0.01 сек.